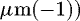| Issue |
Matériaux & Techniques
Volume 106, Number 6, 2018
|
|
|---|---|---|
| Article Number | 604 | |
| Number of page(s) | 14 | |
| Section | Métaux et alliages / Metals and alloys | |
| DOI | https://doi.org/10.1051/mattech/2018058 | |
| Published online | 15 February 2019 | |
Regular Article
On the evaluation of dislocation densities in pure tantalum from EBSD orientation data
Sur l’évaluation des densités de dislocations dans le tantale pur à partir de données d’orientation EBSD
1
LEM3, Université de Lorraine/CNRS/Arts et Métiers ParisTech,
7 rue Félix Savart,
57070
Metz, France
2
Mines ParisTech, CEMEF - Center of Materials Forming, UMR CNRS 7635,
BP 207,
06904
Sophia Antipolis Cedex, France
3
CEA Valduc,
21120
Is-sur-Tille, France
4
ICMMO, UMR CNRS 8182, Université Paris-Sud, Université Paris-Saclay,
91405
Orsay Cedex, France
5
Laboratoire Léon Brillouin, (CEA-CNRS), CEA Saclay,
Gif-sur-Yvette, France
* e-mail: claude.fressengeas@univ-lorraine.fr
Received:
17
September
2018
Accepted:
12
November
2018
We analyze measurements of dislocation densities carried out independently by several teams using three different methods on orientation maps obtained by Electron Back Scattered Diffraction on commercially pure tantalum samples in three different microstructural states. The characteristic aspects of these three methods: the Kernel average method, the Dillamore method and the determination of the lattice curvature-induced Nye’s tensor component fields are reviewed and their results are compared. One of the main features of the uncovered dislocation density distributions is their strong heterogeneity over the analyzed samples. Fluctuations in the dislocation densities, amounting to several times their base level and scaling as power-laws of their spatial frequency are observed along grain boundaries, and to a lesser degree along sub-grain boundaries. As a result of such scale invariance, defining an average dislocation density over a representative volume element is hardly possible, which leads to questioning the pertinence of such a notion. Field methods allowing to map the dislocation density distributions over the samples therefore appear to be mandatory.
Résumé
On analyse les mesures de densités de dislocations effectuées indépendamment par plusieurs équipes en utilisant des méthodes différentes sur des cartes d’orientations obtenues par Electron Back Scattered Diffraction sur des échantillons de tantale commercialement pur dans trois états métallographiques différents. Les trois méthodes utilisées : la méthode du Kernel Average, la méthode de Dillamore et la méthode de détermination des composantes du tenseur de Nye induites par les courbures de réseau sont rappelées et analysées, et les résultats comparés. L’un des aspects essentiels des distributions de densités de dislocations, obtenues dans l’analyse des échantillons, est leur forte hétérogénéité. Des fluctuations de densité de dislocations s’élevant à plusieurs fois leur niveau de base, et s’exprimant en lois-puissance de leur fréquence spatiale sont observées le long des joints de grains et à un moindre degré le long des sous-joints de grains. Il résulte d’une telle absence d’échelle caractéristique que la définition d’une densité de dislocation moyenne sur un élément de volume représentatif pose problème, ce qui conduit à s’interroger sur la pertinence de cette notion. L’emploi de méthodes à champ complet permettant de dresser des cartes de densités de dislocations sur les échantillons analysés semble donc inévitable.
Key words: dislocation density / electron back scattered diffraction / tantalum / grain boundaries / sub-grain boundaries
Mots clés : densités de dislocations / rétrodiffusion électronique / tantale / joints de grains / sous-joints de grains
© C. Fressengeas et al., published by EDP Sciences, 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Measuring and mapping dislocation densities, and the associated stored energy are issues of importance for the quantitative description of recrystallization phenomena. Indeed, several mechanisms are highly dependent on the details of the dislocation density and stored energy distributions in the material. Nucleation of recrystallization occurs in regions of high stored energy; gradients in the stored energy underpin the driving force for the migration of the recrystallization front; the shape of recrystallizing grains and roughness of the recrystallization front are directly controlled by the heterogeneity of the stored energy field. The latter, in turn, influences the capillarity contribution to the driving force. Therefore, a campaign was dedicated to measuring and mapping dislocation densities and/or stored energy within the framework of a French research network on recrystallization funded by CNRS (GDR CNRS 3436, 2010–2014 followed by GDR CNRS 2006, 2017–2021).
The campaign consisted in comparing different means for assessing dislocation densities or stored energy from EBSD-based orientation microscopy (allowing for the assessment of the lattice curvatures) to X-Ray or neutron diffraction (allowing for global measurements or texture component contributions). The model material was commercially pure tantalum, single phase BCC, in different work-hardening states, and therefore with different types of intragranular structures (dislocation tangles or cells). The aim of the present paper is to investigate and discuss, how much information can be obtained from EBSD maps. A forthcoming paper will compare these EBSD results with those of X-Rays and neutron diffraction experiments.
2 Material and metallurgical states
Three metallurgical states have been prepared from an initial 7.7 mm thick sheet of highly pure tantalum (chemical composition given in Tab. 1). The thermomechanical history of that initial sheet ends up with a recrystallization annealing period (at 1050 °C for 2 hours) followed by cold-rolling to about 92% thickness reduction, by successive passes in one direction before changing to the orthogonal direction. The as-received material was then highly work-hardened.
The as-received state was annealed for one hour at 1200 °C under high vacuum to provide a fully recrystallized reference state, therefore, with a much lower dislocation content. Finally, a third metallurgical state was prepared by submitting the fully recrystallized material to a 25% thickness reduction by cold rolling. All three microstructures are illustrated in Figure 1. Since pure tantalum has a strong affinity for oxygen, the chemical composition of all three metallurgical states has been checked (Tab. 1). The reference state is unambiguously fully recrystallized (Fig. 1a). Grains are equiaxed and do not exhibit strong internal FSE or BSE intensity fluctuations and, thus no significant intragranular orientation variations. The grain size distribution (few tens to few hundreds µm) is somewhat heterogeneous throughout the sample, most likely as a result of strain heterogeneity in the as-received work-hardened state. After 25% thickness reduction, the former grains can still be recognized, but intragranular orientation gradients developed during plastic deformation, as a result of strain rate gradients and geometrically necessary dislocations (GNDs) storage. It is worth mentioning here that these gradients appear to be quite continuous (smooth variations in the FSE/BSE intensity inside a given grain), without any obvious sign of sub-grain boundary formation. The deformed grains are therefore very likely to contain GNDs spread out in the whole volume. In the highly strained material (actually the as-received state, Fig. 1c), the BSE orientation contrast shows on the contrary abrupt changes along lines with a characteristic distance (within and below the µm range) that is much smaller than the original grain size. This microstructure is, therefore, very likely to contain sub-grain boundaries and cells resulting from GNDs organization.
Chemical purity of the three investigated metallurgical states [weight ppm].
 |
Fig. 1 Microstructure of the three investigated metallurgical states, as observed in longitudinal sections. The normal direction of the initial sheet is vertical; the (last) rolling direction is horizontal for the two cold-rolled samples. a: Fully recrystallized state; FSE (Forward Scattered Electron) micrograph; b: After 25% thickness reduction by cold rolling; FSE micrograph; c: After 92% thickness reduction by cold rolling; BSE (Back Scattered Electron) micrograph. Both types of micrographs, FSE and BSE exhibit orientation contrast. Microstructures observées dans une section longitudinale pour les trois états métallurgiques étudiés. La direction normale à la tôle dans son état initial est verticale. En (b) et (c), la (dernière) direction de laminage est horizontale. a : État recristallisé ; micrographie FSE ; b : État après réduction de 25 % par laminage à froid ; micrographie FSE ; c : Après réduction de 92 % par laminage à froid ; micrographie BSE. Les deux types de micrographie FSE et BSE présentent un contraste d’orientation. |
3 Experimental details and EBSD data analysis principles
3.1 Sample preparation for EBSD measurements
Longitudinal sections have been prepared for EBSD analysis from the three metallurgical states. The analyses were carried out at the sheets mid-thickness. For accurate and relevant measurement of intragranular misorientations by EBSD, attention must be paid to removing the layer below the analyzed surface, as it was inevitably work-hardened by sawing and mechanical polishing. Sample preparation appeared to be quite challenging for such a pure and therefore ductile metal, and especially for the reference recrystallized samples, but suitable surface quality could be achieved using the following procedure. The deformed materials were prepared by mechanical polishing on SiC griding papers, spending a long time on each grade to ensure the removal of the hardened layer of the previous step (much longer than the time required to simply erase the previous scratches). The final step was a prolonged polishing (more than 15 min) with colloidal silica suspension (so-called OPS by the supplier, Struers), with a light load and a slow rotation speed. For the annealed, much softer material, an additional etching step appeared to be necessary with fluorhydric acid-based etchant.
3.2 EBSD measurements
EBSD maps were obtained for each metallurgical state, by using two distinct equipments operated by two different teams (in order to assess possible fluctuations related to acquisition settings). The data analyzed in Sections 3.3 and 3.5 were acquired at MINES ParisTech using a Zeiss SUPRA 40 FEG-SEM equipped with a Bruker Crystalign system and a sensitive EBSD camera. The data analyzed in Section 3.4 were obtained at Paris Sud University using a Zeiss SUPRA 55 VP FEG-SEM and an EDAX-OIM fast EBSD camera. All data were post-processed using the EDAX-OIM software, but following different principles as detailed below.
3.3 Estimating the GND density from Kernel Average Misorientations
The simplest estimate of the density of geometrically necessary dislocations, ρGND, from EBSD maps is probably the scalar value derived from equation (1) below for particular dislocation structures:
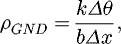 (1)
(1)
where Δθ is the misorientation angle, Δx the distance over which the misorientation is measured, and b the norm of the Burgers vector of the involved/assumed type of dislocations (285 pm in tantalum for ½ < 111> dislocations). The elastic curvature 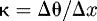 is also a measure of the GND density, referred to below in Section 3.5 as α [1,2], with dimension m−1. The value of the constant k depends on the type of boundary [3,4]: k = 1 if the postulated dislocation structure is a tilt sub-boundary made of edge dislocations, or k = 2 in the case of a twist sub-boundary made of an array of screw dislocations (see a comprehensive justification below in Sect. 3.5). In the present work, we use the first assumption: GNDs are assumed to be mainly edge dislocations, inducing tilt rotations of the crystal lattice.
is also a measure of the GND density, referred to below in Section 3.5 as α [1,2], with dimension m−1. The value of the constant k depends on the type of boundary [3,4]: k = 1 if the postulated dislocation structure is a tilt sub-boundary made of edge dislocations, or k = 2 in the case of a twist sub-boundary made of an array of screw dislocations (see a comprehensive justification below in Sect. 3.5). In the present work, we use the first assumption: GNDs are assumed to be mainly edge dislocations, inducing tilt rotations of the crystal lattice.
From a practical point of view, an EBSD map is composed of discrete orientation data measured at points separated by a distance 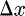 and misoriented by an angle
and misoriented by an angle 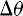 . Hence, full field information on the GND density can be obtained from the curvatures
. Hence, full field information on the GND density can be obtained from the curvatures 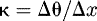 as shown below in Section 3.5. The misorientation angle between neighboring points can also be averaged for each individual point of the map (average of the misorientation angles at neighboring points located within a given distance), which provides the so-called Kernel average misorientation (KAM) value. An estimate of the local GND density can then be calculated from KAM values, accordingly dividing by the step size or by the kernel radius. In the present work, both the KAM-based and full field approaches have been used.
as shown below in Section 3.5. The misorientation angle between neighboring points can also be averaged for each individual point of the map (average of the misorientation angles at neighboring points located within a given distance), which provides the so-called Kernel average misorientation (KAM) value. An estimate of the local GND density can then be calculated from KAM values, accordingly dividing by the step size or by the kernel radius. In the present work, both the KAM-based and full field approaches have been used.
Since orientations and misorientations can only be determined within a certain accuracy range (typically 0.5°) under standard EBSD mapping settings, it is worth mentioning that the lowest misorientations must be excluded from the analysis, since they may correspond to measurement noise. A proper estimate of the noise level is a hard task, since it depends on the acquisition settings as well as on the crystal orientation itself [5]. Here, a simple misorientation angle cut-off threshold will be applied. Attention must also be paid to the fact that the considered reference distance (step size or kernel radius) has a strong influence on the local misorientation or KAM values. Furthermore, it is worth mentioning that the partition between GNDs and statistically stored dislocations (SSDs) is intrinsically dependent on the considered length scale, i.e. on the step size chosen for the EBSD map. The influence of the noise cut-off threshold and of the adopted reference distance on the evaluated GND density will be investigated in the case of the highly deformed material and discussed in Section 4.2.1.
3.4 Estimating the dislocation density from cell analysis (Dillamore approach)
The Dillamore approach (Eq. (2)) consists in estimating the stored energy E associated with dislocations mainly located at the sub-grain boundaries of the deformation cells [6], according to Read-Shockley’s formula. Consequently, the approach neglects the stored energy part linked to the dislocations inside the cells and underestimates the energy of high-angle boundaries. An estimate of the GND density ρGND is then obtained by dividing the stored energy by the elastic energy per unit of dislocation density. The stored energy is postulated as:
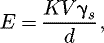 (2)
(2)
where γs is the sub-grain boundary energy, d the deformation cell diameter assuming equiaxed cells [6], V is the molar volume (V = 10.85.10−6m3.mol−1 for pure BCC tantalum) and K is a constant that depends on the shape of the deformation cell. The Read and Shockley grain boundary energy [7] is given by equation (3).
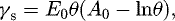 (3)
where
(3)
where 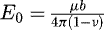 and
and 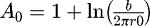 . The values μ = 70 GPa of the shear modulus, ν = 0.35 of the Poisson’s ratio and b = 0.285 nm of the Burgers vector were used in equation (3). The dislocation core radius r0 is classically considered between b and 5b. It can be shown that for BCC iron, r0 = b, so the same value has been chosen for tantalum. Alternatively, the grain boundary energy reads in a slightly different form:
. The values μ = 70 GPa of the shear modulus, ν = 0.35 of the Poisson’s ratio and b = 0.285 nm of the Burgers vector were used in equation (3). The dislocation core radius r0 is classically considered between b and 5b. It can be shown that for BCC iron, r0 = b, so the same value has been chosen for tantalum. Alternatively, the grain boundary energy reads in a slightly different form:
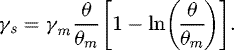 (4)
(4)
It can be plotted as a function of θ (see Fig. 2) and it appears that γm = 0.966 J.m−2 and θm = 23° for tantalum.
From equations (2) and (4), the stored energy E is then given by the relation:
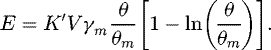 (5)
(5)
In their initial approach, Dillamore et al. [6] only considered equiaxed cells, even if the dislocation cell shape may vary with the crystallographic orientation. Under such conditions, K’ is equal to K/d with K = 3.31. In a more recent work, Samet-Meziou et al. [8] have extended this approach by considering the aspect ratio of lamellar cells, and then shown that K’ can be expressed as:
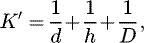 (6)
where d is the width of an elongated cell along the rolling direction, D its length in the transverse direction and h its thickness along the normal direction. These dimensions can be measured from EBSD maps performed in the three orthogonal planes of the sample. Finally, the dislocation density ρGND is calculated from:
(6)
where d is the width of an elongated cell along the rolling direction, D its length in the transverse direction and h its thickness along the normal direction. These dimensions can be measured from EBSD maps performed in the three orthogonal planes of the sample. Finally, the dislocation density ρGND is calculated from:
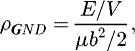 (7)where
(7)where 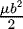 is an elastic energy per unit dislocation density. Using this approach, a value of dislocation density is calculated for each texture component and the overall value is determined by using a mixture law accounting for the volume fractions of the components.
is an elastic energy per unit dislocation density. Using this approach, a value of dislocation density is calculated for each texture component and the overall value is determined by using a mixture law accounting for the volume fractions of the components.
 |
Fig. 2 Boundary energy as a function of the misorientation angle in tantalum. Énergie de joint de grain dans le tantale en fonction de l’angle de désorientation. |
3.5 Determination of Nye’s tensor components from EBSD maps
As suggested above in Section 3.3, a field description of the GND density can be obtained from the maps of discrete orientation data. The method is simply a tensorial extension (i.e. accounting for the orientations) of the scalar estimate provided by the KAM method in Section 3.3. If, Ue denotes the elastic distortion (strain and rotation) tensor, Nye’s dislocation density tensor  is defined at small strains as
is defined at small strains as 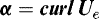 . Decomposing Ue into its symmetric part, i.e. the elastic strain tensor εe, and its skew-symmetric part, i.e. the elastic rotation tensor ωe, is also
. Decomposing Ue into its symmetric part, i.e. the elastic strain tensor εe, and its skew-symmetric part, i.e. the elastic rotation tensor ωe, is also 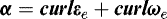 . Introducing the elastic curvature tensor
. Introducing the elastic curvature tensor 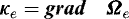 where Ωe is the elastic rotation vector associated with ωe,
where Ωe is the elastic rotation vector associated with ωe, 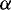 also reads
also reads
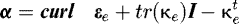 (8)
where
(8)
where 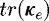 denotes the trace of
denotes the trace of 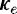 [1,2]. The elastic curvature components
[1,2]. The elastic curvature components 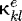 are recovered from finite differences in the EBSD orientation map as
are recovered from finite differences in the EBSD orientation map as 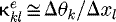 , where the subscripts (k, l) are taken in k ∈ {1, 2, 3} and l ∈ {1, 2}. Hence, six curvature components can be obtained from a single planar orientation map in the plane (x1, x2). In comparing with the KAM method, note that directions are considered here for both the spatial steps and the rotation components. By additionally recovering the elastic strain field and subsequently building
, where the subscripts (k, l) are taken in k ∈ {1, 2, 3} and l ∈ {1, 2}. Hence, six curvature components can be obtained from a single planar orientation map in the plane (x1, x2). In comparing with the KAM method, note that directions are considered here for both the spatial steps and the rotation components. By additionally recovering the elastic strain field and subsequently building 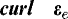 , the dislocation density tensor
, the dislocation density tensor 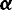 can be obtained from equation (8). Most often however, the curl of the elastic strain is neglected, and
can be obtained from equation (8). Most often however, the curl of the elastic strain is neglected, and 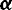 is approximately given by [9–11]:
is approximately given by [9–11]:
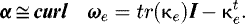 (9)
(9)
The algorithm employed in this paper for calculating the elastic curvature components uses only the first neighbor points and a forward-Euler finite difference scheme for differentiating the elastic rotations. More complex algorithms involving the second or third neighbors were not necessary.
It can be shown from equation (9) that only five dislocation densities can be recovered from the measured curvatures, namely: (α12, α13,α21, α23, α33) in the current sample reference frame [11]. If the dislocation structure is assumed to be a tilt boundary composed for example of edge dislocations 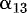 , then equation (9) shows that
, then equation (9) shows that 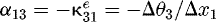 , which justifies choosing k = 1 in the KAM method above in Section 3.3. If conversely, the dislocation structure is assumed to be a twist boundary composed of a cross-grid of screws (α11, α22), then equation (9) leads to
, which justifies choosing k = 1 in the KAM method above in Section 3.3. If conversely, the dislocation structure is assumed to be a twist boundary composed of a cross-grid of screws (α11, α22), then equation (9) leads to 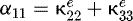 and
and 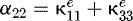 . Overlooking
. Overlooking 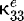 , which cannot be obtained from the data, and defining α as
, which cannot be obtained from the data, and defining α as  motivates choosing k = 2 in equation (1). From these two examples as well as from equation (9) in general, it is clear that the values of the dislocation densities αkl depend on the map’s step size. Indeed, if the lattice misorientation Δθk induced by a crystal defect over a distance Δxl is assigned to an oversized step Δx ’ l > Δxl, then the measured value
motivates choosing k = 2 in equation (1). From these two examples as well as from equation (9) in general, it is clear that the values of the dislocation densities αkl depend on the map’s step size. Indeed, if the lattice misorientation Δθk induced by a crystal defect over a distance Δxl is assigned to an oversized step Δx ’ l > Δxl, then the measured value 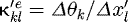 underestimates the actual curvature
underestimates the actual curvature 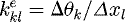 . Furthermore, as already mentioned, oversized steps may lead to crystal defects offsetting each other, which reduces again the measured dislocation density. This dependence will be documented in the next Section, particularly in Figure 5 and Table 3. Note that, if the error on the misorientations is δθ = 0.5° and the minimum misorientationΔθ = 5° and if the error on the spatial location is δx = 1nm for the minimum step size Δx = 38nm in our measurements, then the relative error estimate
. Furthermore, as already mentioned, oversized steps may lead to crystal defects offsetting each other, which reduces again the measured dislocation density. This dependence will be documented in the next Section, particularly in Figure 5 and Table 3. Note that, if the error on the misorientations is δθ = 0.5° and the minimum misorientationΔθ = 5° and if the error on the spatial location is δx = 1nm for the minimum step size Δx = 38nm in our measurements, then the relative error estimate 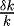 on the generic curvature
on the generic curvature 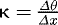 is
is 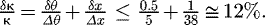 Errors on the misorientation are clearly the most detrimental ones.
Errors on the misorientation are clearly the most detrimental ones.
4 Results
4.1 Microstructure of the three metallurgical states
EBSD maps representative of the three investigated metallurgical states are shown in Figure 3, together with the corresponding pole figures. The ODFs were calculated with the software ATEX [12]. The orientation of each data point was considered in the series expansion method of Bunge [13] up to Lmax = 22. The EBSD maps qualitatively confirm the previous interpretation of the FSE/BSE micrographs in Figure 1. Intragranular crystal orientation is uniform in the recrystallized state but shows smooth gradients after 25% cold rolling, and grains subdivide into disoriented fragments as a result of high strains. The main orientation seems to be characterized by < 111> // ND for all three states, but discussing any global texture evolution based on such small measured areas would be rather reckless.
Intragranular substructures developing during cold rolling can be better depicted using KAM maps (Fig. 4). Figure 4a shows that most grains of the recrystallized material have KAM values in the range of – or below – the accuracy limit (typically 0.5°, blue color), but it also reveals that few grains exhibit higher KAM values. Several explanations can be attempted:
-
the material was in fact not fully recrystallized; this is quite unlikely because the grains with higher KAM values have regular equiaxed shapes;
-
chemical etching performed after polishing was not fully efficient in removing the hardened layer all over the microstructure; work-hardening is orientation-dependent, so the hardened layer is likely to be thicker for some of the grains;
-
due to EBSD indexing procedures, the accuracy is somewhat orientation dependent; this could be another reason for getting higher KAM values only in some grains, but then all the pixels of one concerned grain would have similar values, which is not really the case.
The most convincing explanation is, therefore that the polishing-induced hardened layer has not been completely removed in some grains. The dislocation density of the reference recrystallized state will thus be a bit overestimated due to the remnant sample-preparation-induced work-hardening. It was, nevertheless, decided not to etch the sample further to avoid introducing surface roughness, which would have led to other artefacts and drawbacks.
After 25% cold–rolling (Fig. 4b), substructures start developing, mostly near grain boundaries and near triple junctions. The close-up shown in Figure 4c reveals sets of parallel sub-grain boundaries with a misorientation in the range of 1–2°. Such substructures are much more developed after 92% cold-rolling, most of the former grains being fragmented into well-defined cells (Fig. 4d). The typical size of those cells is in the micron range, and many of the cell walls have misorientations as large as 5–15° (grey lines in Fig. 4d), and even higher (black lines) for few ones.
Resolving the highly deformed substructures required using much smaller step sizes compared to the recrystallized state (2.3 µm, 240 nm and 80 nm in Figs. 3a and 4a, Figs. 3c and 4b, and Figs. 3e and 4d, respectively). This prevents from any direct quantitative comparison of the intragranular misorientations measured in the three metallurgical states. The local disorientation is indeed very much dependent on the distance over which it has been measured. In a constant orientation gradient, it is basically proportional to the step size. On a more general basis, this dependence varies with the substructure type and on the scale over which it develops. The influence of the EBSD grid step size on the estimated dislocation density will be detailed below.
 |
Fig. 3 EBSD maps (orientation color code defined according to the ND projected into the standard triangle) and related pole figures (density color coded; blue for low to red for the highest densities). Thick black lines are boundaries with a disorientation higher than 10°, thin ones have a disorientation in the range 2–10°. a,b: Reference fully recrystallized; c,d: 25% cold-rolled- and; e,f: 92% cold-rolled-samples. Cartes EBSD (code de couleur défini selon la projection de la direction normale ND dans le triangle standard) et figures de pôle correspondantes (le code de couleur indique une densité croissante du bleu vers le rouge). Les traits gras représentent les joints de grains de désorientation supérieure à 10°, les traits minces une désorientation comprise entre 2 et 10°. a,b : État recristallisé ; c,d : État faiblement laminé (réduction de 25 %) ; e, f : État fortement laminé (réduction de 92 %). |
 |
Fig. 4 EBSD maps (color code related to the local misorientation quantified as a KAM value). a: Reference fully recrystallized- ; b,c: 25% cold-rolled- and; d: 92% cold-rolled- samples. Black boundaries have a disorientation higher than 15°, grey ones in the range 5–15°, green ones between 2–5°. Cartes EBSD (code couleur relatif à la désorientation locale quantifiée par la méthode KAM). a : Matériau recristallisé ; b, c : Matériau faiblement laminé (réduction de 25 %); d : Matériau fortement laminé (réduction de 92 %). Les traits noirs représentent les joints de grains de désorientation supérieure à 15°, les traits gris une désorientation comprise entre 5 et 15°, les traits verts une désorientation entre 2 et 5°. |
4.2 GND density estimate from KAM analysis
4.2.1 Influence of step size and of other analysis parameters on the estimated values
The sample area of Figure 3e has been scanned with different step sizes (38, 80, 160 and 360 nm) in order to assess the influence of the spatial resolution on the estimated value of ρGND. Several analysis parameters have been tested also:
-
threshold values of 0.5, 0.75 and 1° have been used for cutting out the low misorientation values (likely due to noise);
-
maximal misorientation angle has to be defined so that the boundaries are not included in the calculation of the KAM, two values were considered, either 5 or 15°;
-
the kernel radius for the calculation of the KAM was set to one or three times the step size, so that the misorientations with the first or third neighbors were considered.
For each case, the KAM distribution histogram was built in the angular range between the “noise” threshold and the “grain boundary” upper limit, and the average value of the distribution < KAM > was calculated. The density of GNDs was then calculated using that averaged value, using equation (1), with < KAM > for Δθ, k = 1 (arbitrary choice, the main dislocation type being a priori unknown), and Δx being the kernel radius.
The sensitivity of the dislocation density to the map’s step size and analysis parameters is shown in Figure 5. Clearly, the calculated ρGND decreases with increasing the map’s step size and the Kernel radius as already pointed out by references [9,14]. Of course, the calculated ρGND also decreases with increasing the threshold for orientation noise cut-off. Overall, the figure shows that, depending on the chosen experimental parameters, the measured dislocation density value may vary by about one order of magnitude.
Additional sources of error intrinsic to the KAM method are the arbitrarily assumed dislocation structure of the sub-grain boundaries and the lack of account of the dislocations associated with grain boundaries, for misorientations higher than 5°. This latter issue becomes detrimental when the material is highly deformed. Other sources of error are the map resolution and the lack of assessment of the lattice curvatures in the normal direction. They are common to the KAM and Nye’s tensor field approaches and will be discussed below in Section 4.4.
 |
Fig. 5 GND density vs. step size for the 92% cold-rolled sample. Overall values obtained from averaged KAM values. The various curves show the influence of the analysis parameters: kernel radius, cutting threshold for noise measurement and maximum local disorientation. Densité de dislocations géométriquement nécessaires en fonction du pas pour le matériau fortement laminé (taux de réduction de 92 %). Valeurs globales sur la cartographie, obtenues à partir de la valeur moyenne du KAM calculé avec différents paramètres d’analyses. Les courbes représentent l’influence sur ces résultats des facteurs d’analyse suivants : pas de la carte EBSD, rayon du noyau, seuil de coupure du bruit de fond et désorientation locale maximum. |
4.2.2 Comparison of GND density estimates for the three metallurgical states
In all three cases shown in Figure 6, the influence of the noise threshold on the dislocation density estimates shown in Figure 5 is qualitatively confirmed. As seen from the polished vs. polished-and-etched recrystallized samples, the impact of the surface preparation quality on the dislocation density measured at the sample surface can be as high as almost two orders of magnitude. For the properly prepared samples, and as expected, the dislocation density measured at sheet mid-thickness increases with the degree of cold rolling, from 25 to 92%. For the 25% cold-rolled sample, an additional EBSD scan has been performed in an area closer to the sheet surface in order to check if any through-thickness heterogeneity (possibly arising from friction between the sheet and the rolling mill) could be detected. The results indeed show that the GND density seems to be somewhat lower close to the sheet surface compared to mid-thickness. Relating the dislocation density to the local effective strain is out of scope in the present paper but deserves further investigation in future work.
 |
Fig. 6 GND density values for the three metallurgical states (Recrystallized, 25% cold-rolled, 92% cold-rolled), as a function of the orientation noise threshold, sample preparation and step size of the orientation map in the 92% cold-rolled case. Densité de dislocations géométriquement nécessaires dans les trois états métallurgiques étudiés (Matériau recristallisé, faiblement laminé (25 % de réduction) et fortement laminé (92 % de réduction), en fonction du seuil de bruit aléatoire sur l’orientation, de la préparation de l’échantillon et du pas de la carte d’orientation dans le cas fortement laminé. |
4.3 GND density estimation by the Dillamore approach
In order to use the Dillamore approach, the main texture orientation fractions have to be measured. Texture characterization was performed for the three samples by neutron diffraction at the Laboratoire Léon Brillouin in CEA/Saclay (France), on the four circle diffractometer 6T1. The Orientation Distribution Function (ODF) was calculated using the discrete ADC method [15] (Labotex software) from the three complete pole figures {110}, {200} and {211}. The texture is mainly composed of three components: {100}<011>, {111}<110> and {111}<112>.
Because the recrystallized sample and the low deformed sample have no clear dislocation substructure, the Dillamore approach was used only for the 92% cold rolled sample. The cell morphology of the three texture components was determined from EBSD maps (300 × 300 μm2, step size 0.1 μm) measured in (RD, ND) and (TD, ND) planes (Figs. 7a and èb). A close-up showing the substructure in the {111}<110> grains is given in Figure 7c.
The measured values of d, h, D and θ (average misorientation over 10 measurements) and the calculated dislocation density (Eq. (7)) are given in Table 2. From these values, it is possible to calculate an overall value of the dislocation density knowing the volume fraction of the three {100}<001>, {111}<110> and {111}<112> texture components. These fractions were calculated from neutron diffraction measurements: 31, 16 and 16%, respectively, with an orientation spread of 15°. The remaining 37% correspond to other texture components, for which it is assumed that the dislocation substructures are similar to those of the closest main crystallographic orientation. Then, taking a wider tolerance in the definition of the three texture components so that they encompass those 37% (in particular the rest of the {111}<uvw> γ-fiber), their volume fractions become 56, 22 and 22%, respectively. Using a mixture law, it becomes then possible to calculate the average dislocation density in the highest cold rolled sample, i.e. about 2.0 ⋅ 1014m−2. In comparison, the KAM approach (first neighbors, 5° misorientation threshold and a 0.5° noise cut-off) gives a value of about 3.5 ⋅ 1014m−2 (see Fig. 5).
 |
Fig. 7 Distribution of <hkl> crystallographic directions//ND in the: a: (RD, ND) plane; b: (TD, ND) plane, and; c: sub-boundaries (>1°) in the {111}<110> grains in the (RD, ND) plane. Distribution des directions cristallographiques <hkl> parallèles à la direction ND dans : a : le plan (RD,ND) ; b : le plan (TD,ND) ; c : sous-joints de grains (de désorientation supérieure à 1°) dans les grains {111}<110> dans le plan (RD, ND). |
Morphological features of dislocation cells, mean misorientation between cells and calculated dislocation density using the Dillamore approach in the main texture components.
4.4 GND density estimation from the Nye tensor components
Complete fields of the available dislocation density components(α12, α21, α13, α23, α33) in the sample reference frame were computed for the three step sizes (38, 80, 160 nm) in the highly cold-rolled microstructure shown in Figure 3e, for which the grain boundaries were defined by misorientations larger than 5°. As it appears that the dislocation distributions are highly heterogeneous, and also for comparison with the other two present approaches where either the dislocations associated with grain boundaries (KAM method) or the dislocations inside the grains (Dillamore method) are discarded from the analysis, the maps were computed by either including or excluding the grain boundary dislocations. Further, the field of the local average 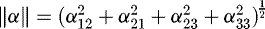 of all measurable components was computed in all cases. As an example, the average measure
of all measurable components was computed in all cases. As an example, the average measure 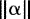 field is shown in Figure 8 for the step size 160 nm when grain boundary dislocations are excluded. At an observation length scale of the order of tens of microns, it appears that the dislocation density is rather evenly distributed throughout the map. Averaging ∥α∥ over the map, we find indeed a value
field is shown in Figure 8 for the step size 160 nm when grain boundary dislocations are excluded. At an observation length scale of the order of tens of microns, it appears that the dislocation density is rather evenly distributed throughout the map. Averaging ∥α∥ over the map, we find indeed a value  . Table 3 provides all such ρGND values for the various cases investigated.
. Table 3 provides all such ρGND values for the various cases investigated.
It can be seen that the density linearly increases when the step size decreases if grain boundary (GB) dislocations are excluded, but varies less than linearly when these dislocations are involved. The average values 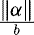 excluding the GB dislocations compare reasonably well with those obtained from the KAM method with only first neighbors, a 5° misorientation threshold and a 0.5° noise cut-off (see Fig. 5). However, the comparison with the computed average density when GB dislocations are included suggests that, although intragranular dislocation densities are not negligible, GB dislocations are much more numerous, which tends to question the Dillamore approach. In addition, the Dillamore value 2.1014 m−2 is significantly less than the grain boundary dislocations value, i.e. the difference (1015–2.1014) m−2 = 8.1014 m−2.
excluding the GB dislocations compare reasonably well with those obtained from the KAM method with only first neighbors, a 5° misorientation threshold and a 0.5° noise cut-off (see Fig. 5). However, the comparison with the computed average density when GB dislocations are included suggests that, although intragranular dislocation densities are not negligible, GB dislocations are much more numerous, which tends to question the Dillamore approach. In addition, the Dillamore value 2.1014 m−2 is significantly less than the grain boundary dislocations value, i.e. the difference (1015–2.1014) m−2 = 8.1014 m−2.
At a smaller scale of the order of microns, heterogeneity is the rule and “hot spots” can be observed in Figure 9 where the density can be as high as 8.1014m−2, approximatively four times the above average value. For illustration of this heterogeneity, maps of the α13 density are provided. They are obtained for the 38 nm step size, i.e. edge dislocations with horizontal Burgers vector and line vector normal to the paper, both in Figure 9 when grain boundary dislocations are excluded and in Figure 10 when they are included in the analysis.
In Figure 10, dislocations are prominently seen at grain boundaries and, in contrast, intragranular dislocations are barely visible. When GB dislocations are masked as in Figure 9, the heterogeneity of their distribution within grains is revealed, and dislocations appear again to be mostly localized in sub-grain boundaries.
 |
Fig. 8 Average dislocation density field (in Champ de densité de dislocation moyenne (en |
Average dislocation density ρGND in m−2 obtained from available Nye’s tensor field components for all step sizes.
 |
Fig. 9 Close-up of the microstructure in Figure 3e, dislocation density component in, 38 nm step size. Space marks in μm. The Burgers vector is horizontal (x1 direction) and the line vector is normal to the paper (x3 direction). Grain boundary dislocations excluded. Note the uneven distribution of these dislocations, mostly at sub-grain boundaries. Agrandissement de la microstructure de la figure 3e. Densité de dislocations en, pas de 38 nm. Les graduations spatiales sont en μm. Le vecteur de Burgers correspondant à ces dislocations est horizontal (direction x1) et le vecteur de ligne normal à la feuille (direction x3). Les dislocations de joints de grains sont exclues. Noter l’hétérogénéité de la distribution des dislocations, qui apparaissent principalement aux sous-joints de grains. |
 |
Fig. 10 Close-up of the microstructure in Fig. 3e, dislocation density component in, 38 nm step size. Space marks in μm. The Burgers vector is horizontal (x1 direction) and the line vector is normal to the paper (x3 direction). Grain boundary dislocations included. Note that dislocations are mostly seen along grain boundaries. Agrandissement de la microstructure de la figure 3e. Densité de dislocations α13 en μm−1, pas de 38 nm. Les graduations spatiales sont en μm. Le vecteur de Burgers correspondant à ces dislocations est horizontal (direction x1) et le vecteur de ligne normal à la feuille (direction x3). Les dislocations de joints de grains sont incluses. Noter l’hétérogénéité de la distribution des dislocations, qui apparaissent principalement aux joints de grains. |
5 Discussion
The strong heterogeneity of the dislocation distributions evidenced above raises the issue of which length scale should be chosen to define average dislocation densities. If the length scale is large, of the order of tens of microns, dislocation offsetting occurs and even if average values of dislocation densities can be defined because some homogeneity of their distribution may be evidenced, they do not accurately reflect lattice incompatibility and the stored elastic energy. If the definition length scale is smaller, of the order of microns in the present case, the heterogeneity of the dislocation distribution is so large between grain boundary, sub-grain boundary areas and the bulk of the material that it cannot be properly reflected by an average value of the dislocation density. At even smaller length scales, dislocation densities reflect accurately particular dislocation patterns, such as dislocation pile-ups or sub-grain boundaries, but they are found in such wide ranges that no single-valued characteristic density is available. Such strongly varying dislocation density distributions, where average dislocation density values can hardly be defined, have been characterized in ice single crystals oriented for basal slip in torsion creep by their scale-invariant character [16], meaning that dislocation density fluctuations are scaling as power-laws of their spatial frequency. Scale-invariance was assigned in the first place to the long-range spatial correlations arising from lattice incompatibility and the associated stored energy, although short-range correlations could be concurrently detected at large strains [16]. Similarly, the distributions of the dislocation density in the present polycrystalline tantalum samples were plotted in Figure 11 in relation with the various microstructures shown in Figure 3. It is seen from this figure that the dislocation densities increase from recrystallized to 25% cold rolled and further to 92% cold rolled, although no characteristic value can be exhibited. Furthermore, the mildly and highly cold-rolled samples also exhibit power-law relationships  between the observed dislocation density and its spatial frequency (defined here as the ratio of the number of patches, where the dislocation density has a certain value in a grid covering the map to the total number of patches in the map), whereas the recrystallized sample does not show such a behavior. This is consistent with the interpretation of the scaling behavior as a manifestation of the long-range spatial correlations arising from lattice incompatibility. Similar conclusions were arrived at in ref [17]. The power-law exponent is of the order of μ = 3 in the 25% cold rolled sample for the 240 nm spatial step of the grid. A study of its variations with the step size in the 92% cold rolled case shows that it varies from μ = 2.17 to μ = 2.84 when the step size decreases from 160 to 38 nm, which indicates, as could be expected, that the dislocation density fluctuations are stronger when the resolution step size becomes smaller. Anyway, μ appears to be smaller than in the 25% cold rolled sample at a comparable step size, which suggests that the dislocation density fluctuations are less strong in the 92% cold rolled sample. Further, the power-law is better defined at moderate deformation in the 25% cold rolled sample than at very large deformation in the 92% cold rolled sample. Such a tendency was also observed in ref [16], where it could be attributed to the existence of more complex spatial correlations at large strains, involving not only long-range elastic correlations between dislocations but also short-range correlations such as cross-slip.
between the observed dislocation density and its spatial frequency (defined here as the ratio of the number of patches, where the dislocation density has a certain value in a grid covering the map to the total number of patches in the map), whereas the recrystallized sample does not show such a behavior. This is consistent with the interpretation of the scaling behavior as a manifestation of the long-range spatial correlations arising from lattice incompatibility. Similar conclusions were arrived at in ref [17]. The power-law exponent is of the order of μ = 3 in the 25% cold rolled sample for the 240 nm spatial step of the grid. A study of its variations with the step size in the 92% cold rolled case shows that it varies from μ = 2.17 to μ = 2.84 when the step size decreases from 160 to 38 nm, which indicates, as could be expected, that the dislocation density fluctuations are stronger when the resolution step size becomes smaller. Anyway, μ appears to be smaller than in the 25% cold rolled sample at a comparable step size, which suggests that the dislocation density fluctuations are less strong in the 92% cold rolled sample. Further, the power-law is better defined at moderate deformation in the 25% cold rolled sample than at very large deformation in the 92% cold rolled sample. Such a tendency was also observed in ref [16], where it could be attributed to the existence of more complex spatial correlations at large strains, involving not only long-range elastic correlations between dislocations but also short-range correlations such as cross-slip.
In this context, we now discuss the main features of the methods used in the present paper for the determination of dislocation density distributions in a benchmark test on tantalum samples. Owing to their strong heterogeneity, field methods seem to be more appropriate to their description, as pointwise average quantities built over small scale domains are very unlikely representative of a typical dislocation density. Indeed, the scaling behavior shown in Figure 11 suggests that Representative Volume Elements as postulated in homogenization procedures can hardly be defined. All three methods: KAM, Dillamore and Nye’s tensor field method use a planar (x1, x2) orientation map and the curvatures 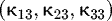 arising from rotation gradients in the normal direction x3 are overlooked. However, this limitation stems from the experimental techniques used for obtaining orientation data sets, not from the data analyses themselves. In particular, Nye’s field method could very well deal with these additional curvatures if 3D orientation maps were available [4,18]. Since they determine the dislocation densities from the associated lattice curvatures, both the KAM and Nye’s tensor methods are inherently sensitive to the step size in the orientation data set. In principle, the optimum step size is of the order of the characteristic length of the crystal defect microstructure producing the misorientation. For example, the step size for evaluating the edge dislocation density along a low-angle tilt boundary should be of the order of, or only slightly larger than, the thickness of the boundary. Larger step sizes lead to underestimating the lattice curvature arising from the boundary. In addition, exceedingly large step sizes may lead to opposite contributions to incompatibility offsetting each other in dislocation microstructure patterns, which tends again to decrease the GND densities. The Dillamore method does not directly rely on measures of the lattice curvature arising from the presence of dislocations, but on evaluating the stored energy density in sub-grain boundaries through Read-Shockley’s model for grain boundary energy. Average dislocation densities are then calculated by assuming a homogeneous distribution of the stored energy on all dislocations. As such, the method relies on various assumptions on the dislocation microstructure (sub-grains are assumed to be free of dislocations and then the stored energy is a priori underestimated) and the homogeneity of its distribution not necessarily satisfied in the present samples. Strikingly, it nevertheless provided orders of magnitude for the dislocation densities in reasonable agreement with the other methods.
arising from rotation gradients in the normal direction x3 are overlooked. However, this limitation stems from the experimental techniques used for obtaining orientation data sets, not from the data analyses themselves. In particular, Nye’s field method could very well deal with these additional curvatures if 3D orientation maps were available [4,18]. Since they determine the dislocation densities from the associated lattice curvatures, both the KAM and Nye’s tensor methods are inherently sensitive to the step size in the orientation data set. In principle, the optimum step size is of the order of the characteristic length of the crystal defect microstructure producing the misorientation. For example, the step size for evaluating the edge dislocation density along a low-angle tilt boundary should be of the order of, or only slightly larger than, the thickness of the boundary. Larger step sizes lead to underestimating the lattice curvature arising from the boundary. In addition, exceedingly large step sizes may lead to opposite contributions to incompatibility offsetting each other in dislocation microstructure patterns, which tends again to decrease the GND densities. The Dillamore method does not directly rely on measures of the lattice curvature arising from the presence of dislocations, but on evaluating the stored energy density in sub-grain boundaries through Read-Shockley’s model for grain boundary energy. Average dislocation densities are then calculated by assuming a homogeneous distribution of the stored energy on all dislocations. As such, the method relies on various assumptions on the dislocation microstructure (sub-grains are assumed to be free of dislocations and then the stored energy is a priori underestimated) and the homogeneity of its distribution not necessarily satisfied in the present samples. Strikingly, it nevertheless provided orders of magnitude for the dislocation densities in reasonable agreement with the other methods.
 |
Fig. 11 Distribution of measurable dislocation density in Recrystallized (pale blue curve), 25% cold rolled (orange curve) and 92% cold rolled (red, green and dark blue curves) samples. The red, green and dark blue curves respectively correspond to the 160, 80 and 38 nm resolution step sizes. Distribution de la densité de dislocations mesurable ∥α∥ dans le matériau recristallisé (courbe bleu clair), faiblement laminé (taux de réduction de 25 %) (courbe orange) et fortement laminé (taux de réduction de 92 %) (courbes rouge, vert et bleu foncé). Les courbes rouge, vert et bleu foncé correspondent respectivement aux pas de résolution spatiale de 160, 80 et 38 nm. |
6 Conclusions
Three methods were used in this paper to determine the characteristics of the dislocation density distribution in tantalum samples in three different microstructural states: KAM, Dillamore and Nye’s tensor methods. These methods are either sensitive to various experimental parameters such as the step size of the maps of orientation data (KAM, Nye’s tensor) or rely on assumptions on the dislocation microstructures investigated (KAM, Dillamore). Perhaps more importantly, one of the main features of the uncovered characteristics of the dislocation density distribution is its strong heterogeneity. Fluctuations in the dislocation densities amounting to several times their base level were observed along grain boundaries and to a lesser degree along sub-grain boundaries. They were characterized by their scale-invariant character, meaning that dislocation density fluctuations are scaling as power-laws of their spatial frequency. As a result, defining an average dislocation density over a representative volume element is hardly possible, which leads to questioning the pertinence of such a notion. Field methods allowing to map the dislocation density distributions over the sample therefore appear to be mandatory. Quantitative comparisons between the various dislocation microstructures arising from recrystallized, slightly or highly cold-rolled samples then become possible on a common basis. Similarly, maps of dislocation density distributions allow finding regions where nucleation of recrystallization occurs and develops. Further, dislocation density mapping should provide information on the driving forces for the motion of recrystallization interfaces, including the curvature-induced driving forces, which directly depend on the heterogeneity of the dislocation density distribution across the interface.
Acknowledgements
Funding from CNRS through GDR 3436, 2010-2014 and GDR 2006, 2017–2021 is gratefully acknowledged. N.B and C.F. wish to thank Anthony Rollett for his role in pushing forward the paper.
References
- J.F. Nye, Some geometrical relations in dislocated crystals, Acta Metall. 1, 153 (1953) [CrossRef] [Google Scholar]
- E. Kröner, Continuum theory of defects, in: Balian R. et al. (Eds.), Physics of defects, Les Houches, Session XXXV, 1980, North Holland Publishing Company, 1981 [Google Scholar]
- L.P. Kubin, A. Mortensen, Geometrically necessary dislocations and strain – gradient plasticity: A few critical issues, Scr. Mater. 48(2), 119 (2003) [CrossRef] [Google Scholar]
- M. Calcagnotto, D. Ponge, E. Demir, D. Raabe, Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD, Mater. Sci. Eng. A 527, 2738 (2010) [CrossRef] [Google Scholar]
- C. Moussa, M. Bernacki, R. Besnard, N. Bozzolo, Statistical analysis of dislocations and dislocation boundaries from EBSD data, Ultramicroscopy 179, 63 (2017) [CrossRef] [Google Scholar]
- I.L. Dillamore, C.J.E. Smith, T.W. Watson, Oriented nucleation in the formation of annealing textures in iron, Met. Sci. J. 1, 49 (1967) [Google Scholar]
- W.T. Read, W. Schockley, Dislocation models of crystal grain boundaries, Phys. Rev. 78, 275 (1950) [CrossRef] [Google Scholar]
- A. Samet-Meziou, A.L. Etter, T. Baudin, R. Penelle, Relation between the deformation substructure after rolling or tension and the recrystallization mechanisms of an IF steel, Mater. Sci. Eng. A 473(1–2), 342 (2008) [CrossRef] [Google Scholar]
- B.S. El-Dasher, B.L. Adams, A.D. Rollett, Viewpoint: Experimental recovery of geometrically necessary dislocation density in polycristals, Scr. Mat. 48, 141 (2003) [CrossRef] [Google Scholar]
- D.P. Field, P.B. Trivedi, S.I. Wright, M. Kumar, Analysis of local orientation gradients in deformed single crystals, Ultramicroscopy 103, 33 (2005) [CrossRef] [Google Scholar]
- W. Pantleon, Resolving the geometrically necessary dislocation content by conventional electron backscattering diffraction, Scr. Mater. 58, 994 (2008) [CrossRef] [Google Scholar]
- B. Beausir, J.-J. Fundenberger, Analysis tools for electron and X-ray diffraction, ATEX-software, Université de Lorraine-Metz, 2017, available at www.atex-software.eu. [Google Scholar]
- H.J. Bunge, Texture analysis in materials science-mathematical methods, Butterworths, London, 1982 [Google Scholar]
- D.P. Field, C.C. Merriman, N. Allain-Bonasso, F. Wagner, Quantification of dislocation structure heterogeneity in deformed polycrystals by EBSD, Model. Simul. Mater. Sci. Eng. 20, 024007 (2012) [CrossRef] [Google Scholar]
- K. Pawlik, J. Pospiech, K. Lucke, The ODF approximation from pole figures with the aid of the ADC method, Textures Microstruct. 14–18, 25 (1991) [CrossRef] [Google Scholar]
- J. Chevy, C. Fressengeas, M. Lebyodkin, V. Taupin, P. Bastie, P. Duval, Characterizing short-range vs. long-range spatial correlations in dislocation distributions, Acta Mater. 58, 1837 (2010) [CrossRef] [Google Scholar]
- B. Beausir, C. Fressengeas, N.P. Gurao, L.S. Toth, S. Suwas, Spatial correlation in grain misorientation distribution, Acta Mater. 57, 5382 (2009) [CrossRef] [Google Scholar]
- P.J. Konijnenberg, S. Zaefferer, S.D. Raabe, Assessment of geometrically necessary dislocation levels derived by 3D EBSD, Acta Mater. 99, 402 (2015) [CrossRef] [Google Scholar]
Cite this article as: Claude Fressengeas, Benoît Beausir, Christophe Kerisit, Anne-Laure Helbert, Thierry Baudin, François Brisset, Marie-Hélène Mathon, Rémy Besnard, Nathalie Bozzolo, On the evaluation of dislocation densities in pure tantalum from EBSD orientation data, Matériaux & Techniques 106, 604 (2018)
All Tables
Morphological features of dislocation cells, mean misorientation between cells and calculated dislocation density using the Dillamore approach in the main texture components.
Average dislocation density ρGND in m−2 obtained from available Nye’s tensor field components for all step sizes.
All Figures
 |
Fig. 1 Microstructure of the three investigated metallurgical states, as observed in longitudinal sections. The normal direction of the initial sheet is vertical; the (last) rolling direction is horizontal for the two cold-rolled samples. a: Fully recrystallized state; FSE (Forward Scattered Electron) micrograph; b: After 25% thickness reduction by cold rolling; FSE micrograph; c: After 92% thickness reduction by cold rolling; BSE (Back Scattered Electron) micrograph. Both types of micrographs, FSE and BSE exhibit orientation contrast. Microstructures observées dans une section longitudinale pour les trois états métallurgiques étudiés. La direction normale à la tôle dans son état initial est verticale. En (b) et (c), la (dernière) direction de laminage est horizontale. a : État recristallisé ; micrographie FSE ; b : État après réduction de 25 % par laminage à froid ; micrographie FSE ; c : Après réduction de 92 % par laminage à froid ; micrographie BSE. Les deux types de micrographie FSE et BSE présentent un contraste d’orientation. |
| In the text | |
 |
Fig. 2 Boundary energy as a function of the misorientation angle in tantalum. Énergie de joint de grain dans le tantale en fonction de l’angle de désorientation. |
| In the text | |
 |
Fig. 3 EBSD maps (orientation color code defined according to the ND projected into the standard triangle) and related pole figures (density color coded; blue for low to red for the highest densities). Thick black lines are boundaries with a disorientation higher than 10°, thin ones have a disorientation in the range 2–10°. a,b: Reference fully recrystallized; c,d: 25% cold-rolled- and; e,f: 92% cold-rolled-samples. Cartes EBSD (code de couleur défini selon la projection de la direction normale ND dans le triangle standard) et figures de pôle correspondantes (le code de couleur indique une densité croissante du bleu vers le rouge). Les traits gras représentent les joints de grains de désorientation supérieure à 10°, les traits minces une désorientation comprise entre 2 et 10°. a,b : État recristallisé ; c,d : État faiblement laminé (réduction de 25 %) ; e, f : État fortement laminé (réduction de 92 %). |
| In the text | |
 |
Fig. 4 EBSD maps (color code related to the local misorientation quantified as a KAM value). a: Reference fully recrystallized- ; b,c: 25% cold-rolled- and; d: 92% cold-rolled- samples. Black boundaries have a disorientation higher than 15°, grey ones in the range 5–15°, green ones between 2–5°. Cartes EBSD (code couleur relatif à la désorientation locale quantifiée par la méthode KAM). a : Matériau recristallisé ; b, c : Matériau faiblement laminé (réduction de 25 %); d : Matériau fortement laminé (réduction de 92 %). Les traits noirs représentent les joints de grains de désorientation supérieure à 15°, les traits gris une désorientation comprise entre 5 et 15°, les traits verts une désorientation entre 2 et 5°. |
| In the text | |
 |
Fig. 5 GND density vs. step size for the 92% cold-rolled sample. Overall values obtained from averaged KAM values. The various curves show the influence of the analysis parameters: kernel radius, cutting threshold for noise measurement and maximum local disorientation. Densité de dislocations géométriquement nécessaires en fonction du pas pour le matériau fortement laminé (taux de réduction de 92 %). Valeurs globales sur la cartographie, obtenues à partir de la valeur moyenne du KAM calculé avec différents paramètres d’analyses. Les courbes représentent l’influence sur ces résultats des facteurs d’analyse suivants : pas de la carte EBSD, rayon du noyau, seuil de coupure du bruit de fond et désorientation locale maximum. |
| In the text | |
 |
Fig. 6 GND density values for the three metallurgical states (Recrystallized, 25% cold-rolled, 92% cold-rolled), as a function of the orientation noise threshold, sample preparation and step size of the orientation map in the 92% cold-rolled case. Densité de dislocations géométriquement nécessaires dans les trois états métallurgiques étudiés (Matériau recristallisé, faiblement laminé (25 % de réduction) et fortement laminé (92 % de réduction), en fonction du seuil de bruit aléatoire sur l’orientation, de la préparation de l’échantillon et du pas de la carte d’orientation dans le cas fortement laminé. |
| In the text | |
 |
Fig. 7 Distribution of <hkl> crystallographic directions//ND in the: a: (RD, ND) plane; b: (TD, ND) plane, and; c: sub-boundaries (>1°) in the {111}<110> grains in the (RD, ND) plane. Distribution des directions cristallographiques <hkl> parallèles à la direction ND dans : a : le plan (RD,ND) ; b : le plan (TD,ND) ; c : sous-joints de grains (de désorientation supérieure à 1°) dans les grains {111}<110> dans le plan (RD, ND). |
| In the text | |
 |
Fig. 8 Average dislocation density field (in Champ de densité de dislocation moyenne (en |
| In the text | |
 |
Fig. 9 Close-up of the microstructure in Figure 3e, dislocation density component in, 38 nm step size. Space marks in μm. The Burgers vector is horizontal (x1 direction) and the line vector is normal to the paper (x3 direction). Grain boundary dislocations excluded. Note the uneven distribution of these dislocations, mostly at sub-grain boundaries. Agrandissement de la microstructure de la figure 3e. Densité de dislocations en, pas de 38 nm. Les graduations spatiales sont en μm. Le vecteur de Burgers correspondant à ces dislocations est horizontal (direction x1) et le vecteur de ligne normal à la feuille (direction x3). Les dislocations de joints de grains sont exclues. Noter l’hétérogénéité de la distribution des dislocations, qui apparaissent principalement aux sous-joints de grains. |
| In the text | |
 |
Fig. 10 Close-up of the microstructure in Fig. 3e, dislocation density component in, 38 nm step size. Space marks in μm. The Burgers vector is horizontal (x1 direction) and the line vector is normal to the paper (x3 direction). Grain boundary dislocations included. Note that dislocations are mostly seen along grain boundaries. Agrandissement de la microstructure de la figure 3e. Densité de dislocations α13 en μm−1, pas de 38 nm. Les graduations spatiales sont en μm. Le vecteur de Burgers correspondant à ces dislocations est horizontal (direction x1) et le vecteur de ligne normal à la feuille (direction x3). Les dislocations de joints de grains sont incluses. Noter l’hétérogénéité de la distribution des dislocations, qui apparaissent principalement aux joints de grains. |
| In the text | |
 |
Fig. 11 Distribution of measurable dislocation density in Recrystallized (pale blue curve), 25% cold rolled (orange curve) and 92% cold rolled (red, green and dark blue curves) samples. The red, green and dark blue curves respectively correspond to the 160, 80 and 38 nm resolution step sizes. Distribution de la densité de dislocations mesurable ∥α∥ dans le matériau recristallisé (courbe bleu clair), faiblement laminé (taux de réduction de 25 %) (courbe orange) et fortement laminé (taux de réduction de 92 %) (courbes rouge, vert et bleu foncé). Les courbes rouge, vert et bleu foncé correspondent respectivement aux pas de résolution spatiale de 160, 80 et 38 nm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.