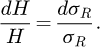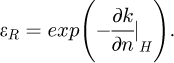EDP Sciences logo
Authentification abonné
Rechercher
Menu
Accueil Tous les numéros Volume 110 / Numéro 2 (2022) Matériaux & Techniques, 110 2 (2022) 205 Full HTML
Numéro
Matériaux & Techniques
Volume 110, Numéro 2, 2022
Special Issue on ‘Indentation across scales and techniques: recent advances in experiments and modelling’, edited by Vincent Keryvin
Numéro d'article 205
Nombre de pages 16
Section Essais, mesure, contrôle non destructif / Testing, measurement and non destructive testing
DOI https://doi.org/10.1051/mattech/2022025
Publié en ligne 4 juillet 2022

© A. Albayda et al., 2022

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

L’essai d’indentation instrumentée est actuellement largement utilisé pour diverses applications et à différentes échelles (macro, micro et nanomètre). Il a été montré que ce test mécanique local permet non seulement l’obtention de la dureté [1–3] mais aussi de prédire une loi d’écrouissage associée au comportement élasto-plastique de matériaux homogènes ou hétérogènes [3–6]. Différentes formes d’indenteurs peuvent être utilisées : sphériques, coniques à base circulaire, Vickers, Berkovich… Quelle que soit la forme de l’indenteur ou l’échelle de l’indentation, l’identification des paramètres mécaniques du matériau indenté s’obtient à partir d’une courbe F(h) mesurée au cours de l’essai, courbe correspondant à l’évolution de la force (F) appliquée par l’indenteur en fonction de l’enfoncement (h) de l’indenteur, ou/et à partir de l'empreinte post mortem laissée en surface du matériau indenté [7–9].

Pour le cas de l’indentation sphérique, la dureté du matériau est obtenue à partir de l’équation (1) proposée par Meyer [10] en 1951 : (1)

où H est la pression de contact (dureté), FMax est la charge maximale appliquée sur l'échantillon, et a est le rayon de contact ou le rayon de l’empreinte. Dans la pratique, a peut être déterminé à partir d’une image optique de l'empreinte après chaque essai d’indentation ou peut être déduit de la courbe d’indentation F(h) [11].

Pour la détermination des propriétés plastiques à partir de l’essai d’indentation, différentes approches peuvent être suivies. Pour la plupart de ces approches, le concept de déformation représentative est utilisé pour construire la loi d’écrouissage du matériau.

Dans le cas d’indentation sphérique, de nombreuses définitions de déformations représentatives ont été proposées dans la littérature. On peut les classer dans deux grandes familles de méthodes : la première famille consiste à atteindre les propriétés plastiques du matériau à partir de la courbe F(h) [12–16], et la deuxième est basée sur la mesure de la pression moyenne de contact d’indentation (H) [7–9,17,18].

La première famille, issue de grandeurs mesurées en indentation instrumentée, repose sur l’hypothèse d’une forme particulière de la loi d’écrouissage du matériau à caractériser. Pour la plupart des méthodes de cette famille, le matériau est supposé avoir une loi de comportement élasto-plastique isotrope à écrouissage isotrope avec comme critère de plasticité celui de Von Mises. Concernant la loi d’écrouissage, le matériau est supposé avoir une loi d’écrouissage isotrope de type Hollomon : (2)

L’identification de la loi d’écrouissage consiste donc à déterminer deux paramètres : la limite d’élasticité initiale σy et le coefficient d’écrouissage n (le module de Young E étant supposé être connu).

Les études basées sur l’étude de la courbe F(h) ont conduit, par un calcul adimensionnel et par simulation par éléments finis, à la détermination d’une déformation représentative qui permet de relier ces deux inconnues de la loi d’écrouissage aux grandeurs mesurées en indentation (force, profondeur de pénétration, énergie). Cette déformation représentative est obtenue de manière mathématique et n’a que très peu de sens physique. Soulignons aussi que la loi de Hollomon ne représente pas toujours la loi d’écrouissage réelle de tous les matériaux.

De manière générale, plus la loi d’écrouissage d’un matériau est fidèle à la loi d’Hollomon, plus l’identification par indentation des valeurs des paramètres de cette loi est précise.

Une loi d’écrouissage de type Hollomon est de manière générale la plus adaptée pour des matériaux métalliques recuits (de faible valeur de limite d’élasticité, et d’écrouissage relativement élevé surtout pour les faibles valeurs de déformation plastique). Pour ces matériaux et pour d’autres matériaux « doux », l’identification des paramètres de la loi d’écrouissage de type Hollomon par indentation amène généralement à de bons résultats [6,19–21].

Pour des matériaux pré-écrouis pour lesquels une loi d’écrouissage de type Voce ou Ramberg–Osgood est plus adaptée, l’identification effectuée à partir de l’indentation, en utilisant une loi d’écrouissage de type Hollomon, a généralement comme conséquence une sous-estimation de la valeur de la limite d’élasticité et une surestimation de l’exposant d’écrouissage [22,23]. C’est le cas aussi pour des aciers présentant un vieillissement et donc la présence d’un palier de Piobers–Lüders sur la courbe de traction [20,24,25].

Pour certains aciers inoxydables ou certains laitons par exemple, pour lesquels la loi d’écrouissage est très linéaire, et donc très différente d’une loi de type puissance, l’identification par indentation en se basant sur une loi d’écrouissage de type Hollomon n’est pas adaptée [20,24].

Malgré le fait qu’elle soit inadaptée pour certains matériaux, la loi d’écrouissage d’Hollomon est cependant généralement utilisée puisqu’elle ne comporte que deux paramètres d’écrouissage à identifier (σy et n). L’avantage de n’avoir que deux paramètres à identifier par indentation est qu’en absence d’imprécision expérimentale et d’hétérogénéité du matériau, l’unicité de solution est garantie lorsque cette identification est effectuée à partir d’une courbe d’indentation ou de plusieurs empreintes [26].

Lorsque la déformation représentative est obtenue à partir de la courbe F(h) [9,13–16,19], la valeur de la déformation représentative obtenue est extrêmement faible et ne dépasse pas une valeur d’ordre de 7 % même pour des profondeurs de pénétration élevée (h de l’ordre de 0 ; 3 fois le rayon de l’indenteur, R).

La deuxième famille de méthode consiste à effectuer des essais de dureté à différentes charges et à construire la courbe d’écrouissage « point par point » du matériau testé à partir de la mesure du rayon de l’empreinte. Aucun type de loi d’écrouissage n’est imposé arbitrairement, mais la déformation représentative est définie cette fois-ci de manière empirique.

Dans le cas de la détermination de la loi d’écrouissage à partir de la dureté H, les premiers travaux portant sur la notion de déformation représentative en indentation sphérique sont effectués par Tabor [7]. Dans un régime d’indentation considéré comme purement plastique, Tabor suppose que le rapport entre la dureté Meyer (Pm ou H) et la contrainte d’écoulement σR est constant. Ce rapport appelé facteur de confinement, noté Cf, est égal à : 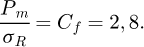(3)

Tabor a défini sa déformation représentative à partir de ce facteur de confinement constant. Pour un indenteur de rayon R et pour un rayon de contact a, la déformation représentative définie par Tabor est égale à : (4)

En se basant sur l’étude de Tabor, Ahn et Kwon [8] ont proposé une nouvelle définition de la déformation représentative de l’indentation sphérique (Éq. (5)). Dans cette définition, la contrainte représentative est proportionnelle à la pression et la déformation représentative dépend de la déformation de cisaillement maximale obtenue au niveau du rayon de contact entre l’indenteur et le matériau indenté. 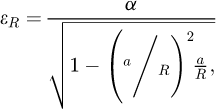(5)

où α est un coefficient plastique constant fixé à 0,1 par Ahn et Kwon [8] pour un facteur de confinement Cf égal à 3.

Pour Jeon et al. [9,17] bien que la méthode proposée par Ahn et Kwon [8] produise des résultats relativement bons par rapport aux essais de traction uniaxiale, les paramètres fixés n’ont pas été optimisés par des méthodes numériques ou théoriques. À partir de plusieurs simulations par éléments finis effectués sur 38 types de matériaux métalliques différents, Jeon et al. [14] montrent que la déformation représentative conduit à de meilleurs résultats lorsque α est égal à 0,14 pour un facteur de confinement Cf toujours égal à 3.

Clairement, la définition de la déformation représentative ne repose pas sur des notions physiques claires. Soit, elle est définie de manière mathématique pour le cas des méthodes basées sur l’ajustement de la courbe F(h) d’indentation à celles obtenues numériquement ou expérimentalement, soit, elle est définie de manière empirique en supposant l’existence d’une constante universelle indépendante des propriétés mécaniques des matériaux indentés.

Dans ce travail, nous focalisons notre étude sur les méthodes basées sur la mesure de la pression moyenne de contact H. Une nouvelle définition de déformation représentative pour le cas d’indentation sphérique est introduite. L’application de cette déformation représentative est validée pour un modèle dérivable, rapide et fiable en considérant plusieurs types de matériaux pseudo-numériques. Une application expérimentale est présentée par la suite. Pour cette application, la loi d’écrouissage obtenue à partir du test d’indentation est comparée avec la loi d’écrouissage obtenue par un essai de traction uniaxial.

2 Discussion sur les méthodes basées sur la pression moyenne de contact

Les méthodes basées sur la pression moyenne de contact consistent à construire la loi d’écrouissage du matériau « point par point » à partir de différents essais d’indentation et à différentes charges. L’avantage de ces méthodes basées sur la mesure de la dureté est qu’elles permettent de construire une loi d’écrouissage quelconque sans faire d’hypothèse sur la forme mathématique de cette loi. Pour la plupart de ces méthodes, il existe un facteur de confinement, Cf, considéré par hypothèse comme étant une constante universelle, qui relie la pression moyenne de contact d’indentation à la contrainte d’écoulement du matériau indenté. Comme il a été mentionné dans l’introduction, il est difficile d’attribuer un sens physique à cette déformation représentative. L’existence d’un facteur de confinement constant reliant la pression moyenne de contact d’indentation à la contrainte d’écoulement représentative a été critiquée de nombreuses fois dans la littérature [18,20]. Pour le cas d’indentation sphérique, la valeur de Cf dépend du matériau étudié et du régime de déformation que subit ce matériau lors de l’indentation sphérique.

Chaudhri [27] a montré que lorsque le rapport 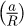augmente, le facteur de confinement décroît dans le cas d’un cuivre polycristallin recuit. La déformation représentative proposée par Chaudhri correspond à la déformation plastique maximale εp,max mesurée sous l’indenteur sphérique (Éq. (6)). Avec cette déformation représentative, le facteur de confinement Cf décroît graduellement quand le rapport a/R augmente. Cf est environ égal à 2,5 lorsque a/R = 0,08, et atteint une valeur environ égale à 1,4 lorsque a/R = 0,85. 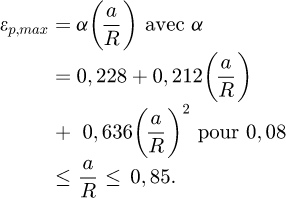(6)

Bartier et al. [28] confirment à partir de résultats de simulation numérique que Cf n’est pas constant. Pour le cas de deux matériaux élasto-plastique écrouissable et parfaitement plastique, Bartier et al. [28] ont montré que Cf augmente lorsque le rayon de contact augmente dans un régime d’indentation élasto-plastique, puis diminue dans un régime dit « purement plastique ».

3 Méthode de détermination de la déformation représentative proposée (méthode du gradient)

La nouvelle définition de déformation représentative proposée pour l’indentation sphérique repose sur des calculs de gradients de dureté. La démarche de détermination de cette déformation représentative est basée sur celle proposée par Hernot et al. [29] dans le cas de l’indentation conique. Elle repose sur l’hypothèse que le matériau présente une loi d’écrouissage décrit par la loi de Hollomon.

Comme l’a proposé Tabor, les notions de déformation représentative et de contrainte représentative permettent de définir le facteur de confinement par la relation : 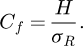(7)

À la différence de Tabor [7] et Ahn et Kwon [8], nous supposons que ce facteur n’est constant que pour un rapport donné. Pour un rapport 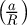donné, la différentielle de Cf étant nulle, on peut écrire : 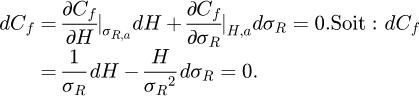(8)

Ce qui donne : (9)

L’équation (9) montre donc qu’il existe une proportionnalité entre la variation de la dureté H et la variation de la contrainte représentative σR. Avec cette proportionnalité, la détermination de l’évolution de H et σR en fonction de σy/E et n montrerait que les iso-valeurs de la dureté H correspondent aux iso-valeurs de σR.

Modifions l’écriture de loi d’Hollomon donnée dans l’équation (2) et appliquons cette équation aux contraintes et déformations représentatives : 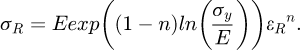(10)

Introduisons le paramètre k tel que 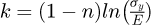, la contrainte représentative devient alors égale à : 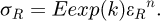(11)

En considérant le module de Young constant, la différentielle de la contrainte représentative σR s’écrit : (12)

L’équation (12) montre donc que : (13)

À partir de l’équation de proportionnalité (9) entre la variation de la dureté H et la variation de la contrainte représentative σR, on peut écrire dans le cas de l’indentation sphérique que pour un rapport a/R : (14)

k étant une fonction implicite de n, le théorème des fonctions implicites permet d’écrire que : 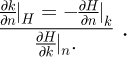(15)

Ce qui donne : (16)

L’équation (16) montre que cette déformation représentative ainsi définie est seulement dépendante des propriétés mécaniques du matériau indenté et ne repose pas sur hypothèse de l’existence d’une constante universelle qui relie la déformation représentative au rapport adimensionnel 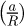. Le vecteur 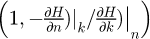étant un vecteur tangent au iso-valeurs de dureté H obtenues pour un même rapport a/R, cette déformation représentative dépend donc localement dans le plan (n, k) de la tangente de ces iso-valeurs de duretés.

Plusieurs étapes de calcul sont requises pour que la méthode de gradient proposée puisse être appliquée. Chaque étape consiste à créer un gradient de dureté choisis de manière précise dans l’espace k et n. Un gradient de dureté est obtenu en perturbant la valeur k du matériau testé pour une même valeur de a et de n, alors qu’un autre gradient de dureté est obtenu avec une perturbation de la valeur n mais cette fois-ci pour une même valeur de k et de a (Éq. (14)).

4 Modèle d’application

Une nouvelle méthode de détermination de la déformation représentative vient d’être définie. La détermination de la déformation représentative par cette méthode dépend de plusieurs facteurs, la valeur de la perturbation des propriétés mécaniques, le matériau lui-même et le modèle d’application qui permet d’obtenir la réponse du matériau à l’indentation. Pour le choix du modèle d’application, le logiciel commercial par éléments finis Abaqus/standard (ver. 6.13) [30] a été choisi comme première application. Le modèle axisymétrique EF a été choisi pour une simulation d’un test d’indentation sphérique (Fig. 1). L’indenteur choisi est sphérique et rigide de rayon 0,25 mm. Onze mille sept cent soixante-quatre éléments axisymétriques à 4 nœuds (CAX4) sont utilisés pour modéliser l’échantillon avec un affinement de la taille des éléments dans la région située au niveau du contact indenteur/matériau. La taille des éléments dans cette région est égale à 1,852 µm. Les éléments trapézoïdaux sont utilisés dans les régions de transition de taille d’élément afin d’empêcher la discontinuité des contraintes et des déformations. La condition de contact est établie en supposant un contact « surface to surface » entre la surface de l’échantillon et l’indenteur avec un coefficient de frottement µ = 0,1.

Un matériau pseudo-numérique écrouissable qui suit parfaitement la loi d’Hollomon (Tab. 1) a été utilisé. Comme le montre l’équation (14), la déformation représentative d’indentation liée à la pression moyenne est obtenue à partir des gradients de dureté calculés en fonction de n et k pour un même rayon de contact. En affectant un incrément de 2,16 % sur les valeurs de n et k et en utilisant les résultats bruts issus des simulations numériques par éléments finis, la déformation représentative décrite par la méthode du gradient est très bruitée (Fig. 2). Ce bruit provient de problèmes numériques au niveau des sorties de données d’Abaqus après simulation. L’imprécision du calcul est due particulièrement à l’imprécision du rayon de contact mesuré par éléments finis et aux valeurs des incréments appliqués sur les valeurs de n et k pour obtenir les gradients de dureté. Un lissage de la courbe d’évolution du rayon de contact en fonction de la profondeur de pénétration permet, en effet, d’atténuer considérablement le bruit obtenu sur l’évolution de la déformation représentative (voir Fig. 2).

Pour résoudre ce problème numérique lié au calcul de gradient, et pour valider la méthode proposée, une application sur un modèle analytique dérivable est une alternative. Dans la littérature, il existe plusieurs modèles analytiques qui prédisent les grandeurs physiques en indentation [1,12,31–35] en fonction des propriétés mécaniques des matériaux utilisées. Dans notre cas, un modèle analytique permettant d’obtenir la dureté en fonction de la surface de contact est nécessaire. Le modèle de Lee et al. [31] proposé en 2005 est un bon candidat car c’est un modèle analytique complet qui été validé dans plusieurs articles [2,31].

Lee et al. [23] ont établi des relations analytiques permettant de relier les paramètres de la loi de comportement du matériau indenté aux grandeurs imposées et mesurées en indentation (force, profondeur de pénétration, hauteur de contact, rayon de contact et diamètre de l’indenteur). Pour ce qui concerne le matériau indenté, les relations proposées ont été obtenues à partir de calculs par éléments finis effectués avec un coefficient de Poisson de 0,3 et les paramètres mécaniques donnés dans le tableau 2. Les auteurs ont proposé des algorithmes numériques permettant de déterminer les propriétés mécaniques à partir de la courbe F(h) obtenue lors d’un essai d’indentation sphérique. Dans le cas de courbes d’indentation obtenues numériquement pour des pseudo-matériaux, l’analyse inverse conduit à l’obtention correcte du module de Young, de la limite d’élasticité et du coefficient d’écrouissage du matériau indenté, ce qui montre la pertinence des relations proposées [36].

La formulation du modèle de Lee est résumée ci-dessous. Pour cette formulation, la loi de puissance de type Hollomon est choisie pour représenter la loi d’écrouissage du matériau indenté ; l’indenteur a une loi de comportement élastique (E = 537 000 MPa, ν = 0,24) et un coefficient de frottement de 0,1 est fixé au niveau du contact matériau–indenteur.

Lors d’un essai d’indentation, l’apparition d’un bourrelet ou d’un enfoncement au niveau du rayon de contact rend difficile la mesure et la prédiction précise du diamètre de contact réel d. Pour un indenteur sphérique rigide de diamètre D, le diamètre de contact réel d peut être évalué à partir de l’équation suivante : 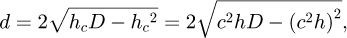(17)

où hc est la hauteur de contact, h est la profondeur de pénétration mesurée à partir de la surface de référence et c 2 est le rapport entre h et hc (c 2 = hc/h) [33]. Dans leur modèle, Lee et al. [19] ont exprimé c 2 comme une fonction de la profondeur d’indentation h, du diamètre de l’indenteur D, et des propriétés mécaniques du matériau indenté : 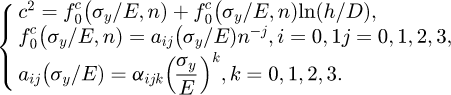(18)

Quarante coefficients αijk ont été obtenus par optimisation afin de déterminer la relation entre la profondeur de pénétration h, et la hauteur de contact hc.

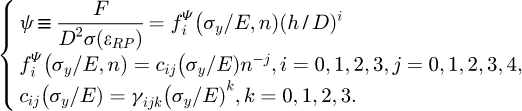Afin de déterminer les propriétés plastiques à partir d’une courbe d’indentation F(h), Lee et al. [23] proposent de déterminer la déformation représentative plastique à partir de l’équation (19), et la contrainte représentative à partir de l’équation (20). (19) (20)

L’expression de la déformation représentative plastique εRP proposée par Lee et al. fait intervenir 80 coefficients βijk et conduit à des valeurs de déformation représentative de l’ordre de 20 % lorsque le rapport h/R atteint la valeur 0,12. L’expression permettant de déterminer la contrainte représentative, σ(εRP), fait aussi intervenir 80 coefficients γijk.

Les expressions analytiques proposées par Lee et al. [23] ont été obtenues de manière totalement empirique à partir de résultats de simulations numériques par éléments finis. Précisons que les simulations par éléments finis de l’indentation sphérique étant effectuées jusqu’à un rapport h/R égal à 0,12, toutes les expressions proposées par Lee et al. [23] ne sont pas vérifiées pour h/R > 0,12. Pour information, cette valeur de h/R correspond à un rayon de contact adimensionnel, a/R, proche de 0,5 lorsqu’il ne se produit aucun bourrelet et aucun affaissement de la surface du matériau indenté située autour de l’empreinte.

thumbnail Fig. 1

Modèle EF axisymétrique pour une indentation sphérique avec des éléments CAX4.

Axisymmetric FE model for spherical indentation with CAX4 elements.
thumbnail Fig. 2

Évolution bruitée de la déformation représentative en fonction du rayon de contact adimensionnel (a/R) obtenue par simulation EF à partir de la méthode du gradient de dureté pour une perturbation de ± 2,16 % pour k et ± 2,16 % pour n.

Noise evolution of the representative strain as a function of the dimensionless contact radius (a/R) obtained by FE simulation from the hardness gradient method for a perturbation of ± 2.16% for k and ± 2.16% for n.
Tableau 1

Propriétés mécaniques du pseudo-matériau utilisé pour montrer le signal bruité du gradient de dureté obtenu par élément finis.

Mechanical properties of the pseudo-material used to show the noisy signal of the hardness gradient obtained by finite element.

Tableau 2

Valeurs des paramètres mécaniques de matériaux indentés utilisés pour la détermination du modèle proposé par Lee et al. [31].

Values of mechanical parameters of indented materials used for determination of the model proposed by Lee et al. [31].

5 Identification à partir de données issues de simulations numériques

Le modèle de Lee [31] a été reprogrammé sous Python [37] pour être facilement exécutable et permettre d’obtenir rapidement des résultats. Le module de Young du matériau indenté et le diamètre de contact d sont supposés être connus pour chaque effort F appliqué par l’indenteur sur le matériau indenté. C’est donc à partir de la dureté H = 4F/(πd2) que l’identification est effectuée à partir des équations (18)–(20).

5.1 Procédure d’identification

Comme première application analytique, un pseudo-matériau numérique dont la loi d’écrouissage suit parfaitement la loi de Hollomon et ayant les propriétés suivantes E = 210 GPa, σy = 100 MPa, n = 0,3 est utilisé. L’indenteur sphérique a un rayon R = 0,25 mm et a les mêmes propriétés mécaniques de l’indenteur semi-rigide étudié par Lee et al. [23] : Eind = 537 GPa et νind = 0,24.

Seuls deux rayons de contact a1 et a2, équivalents à des valeurs de 0,2 R et à 0,3 R, sont utilisés dans un premier temps pour simplifier la présentation de la démarche suivie (Fig. 3). Deux valeurs de forces, F1 et F2, sont calculées avec le modèle analytique proposé par Lee et al. [23], ce qui permet d’obtenir deux valeurs de dureté, H1 et H2. Comme le montre la figure 3, les forces estimées à l’aide du code Python et du modèle de Lee et al. [23] se situent sur la courbe F(a) obtenue par éléments finis pour le matériau pseudo-numérique étudié. Ce résultat valide la programmation en Python effectuée et le modèle de Lee et al. [23] utilisé.

Une fois les duretés sont obtenues, on considère que les valeurs σy et n solution du problème, sont inconnues. Pour rechercher ces deux valeurs, on trace les iso-valeurs de dureté obtenue pour les deux valeurs de dureté H1 et H2, calculées précédemment en fonction des valeurs de σy et de n du matériau indenté. Les pas de cette grille peuvent être modifiés à tout instant. Pour cet exemple, un pas de 10 MPa a été choisi pour σy et 0,005 pour n. On remarque dans la figure 4a que les iso-valeurs de duretés se croisent en un point de coordonnées (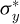 et n*) correspondant à la solution du problème. Comme la loi d’Hollomon est la loi d’écrouissage du pseudo-matériau choisi, on peut tracer les iso-valeurs de dureté dans un nouvel espace [k, n], où k est un paramètre déduit de la loi de Hollomon (Éq. (11)). Dans le nouvel espace, les iso-valeurs de dureté ont une forme linéaire (Fig. 4b). La méthode de gradient (Éq. (14)) est appliquée en créant des gradients de dureté au point « solution » à partir des 2 iso-valeurs de duretés obtenues, ce qui a pour conséquence la détermination de deux déformations représentatives εR1 et εR2 associées à H1 et H2, respectivement. En utilisant l’abscisse et l’ordonnée du point d’intersection des 2 iso-valeurs de dureté, c’est-à-dire et n*, on obtient deux valeurs de contraintes représentatives via l’équation (10). À partir de cette identification, on peut obtenir deux points de la vrai courbe contrainte–déformation.

À partir du modèle analytique, la méthode du gradient peut être appliquée pour autant d’efforts et rayons de contact mesurés que l’on désire. À partir de l’ensemble des rayons de contact et efforts mesurés, deux rayons de contact et efforts considérés amènent à un point d’intersection d’iso-valeurs de dureté. À partir de chaque point d’intersection, deux valeurs de déformation représentative et deux points de la courbe contrainte-déformation du matériau sont ainsi obtenus.

thumbnail Fig. 3

Comparaison entre les efforts obtenus pour deux rayons de contact (0,2 R et 0,3 R) avec le modèle analytique de Lee et al. [31] programmé sous Python et la courbe F(a) obtenue par EF (pseudo matériau : E = 210 GPa, σy = 100 MPa, n = 0,3).

Comparison between the forces obtained for two contact radius (0.2 R and 0.3 R) with the analytical model of Lee et al. [31] programmed in Python and the F(a) curve obtained by FE (pseudo material: E = 210 GPa, σy = 100 MPa, n = 0.3).
thumbnail Fig. 4

Iso-valeurs de dureté obtenues pour deux rayons de contact égal à 0,2 R et 0,3 R. (a) Représentation dans l’espace [σy, n] ; (b) Représentation dans l’espace [k, n].

Hardness iso-values obtained for two contact radii equal to 0.2 R and 0.3 R. (a) Representation in [σy, n] space; (b) Representation in [k, n] space.

5.2 Comparaison avec les différentes déformations et contraintes représentatives proposées dans la littérature

Dans cette partie, nous allons nous baser sur le modèle analytique programmé pour prédire l’évolution de la déformation représentative en fonction du rapport a/R pour deux types de matériaux différents : un matériau doux et un matériau dur dont les propriétés mécaniques sont illustrées dans le tableau 3. Différentes définitions de déformation représentative sont utilisées et comparées. L’évolution du facteur de confinement en fonction du rapport a/R pour chaque définition est présentée par la suite ainsi que l’influence de ce facteur sur la loi d’écrouissage des matériaux.

Pour chaque matériau, 7 mesures de rayon de contact sont utilisées afin d’avoir des rapports compris entre 0,2 et 0,5 (0,2 ; 0,25 ; 0,3 ; 0,35 ; 0,4 ; 0,45 et 0,5). Chaque mesure permet d’obtenir une valeur de dureté et donc une valeur de déformation représentative.

L’évolution de la déformation représentative en fonction du rapport est représentée dans la figure 5. Si l’on compare par rapport aux autres déformations représentatives présentées dans la figure 5, les déformations représentatives proposées par Lee et al. [31] et par Chaudhri [18] en fonction de sont globalement les plus élevées.

Pour un rapport a/R de 0,5, les valeurs de déformation représentatives atteignent 19 % et 25 % de déformation respectivement pour Lee et al. [31] et Chaudhri [18]. La méthode du gradient proposée dans cet article conduit à des valeurs de déformations situées entre celles proposées par Tabor [7] (Éq. (4)) et par Ahn et Kwon [8] (Éq. (5)). La figure 5 montre aussi que pour un matériau doux, l’évolution de la déformation représentative en fonction de a/R, obtenue par la méthode du gradient, n’est pas linéaire au contraire de celles proposées par Tabor ou par Ahn et Kwon [8] et Jeon et al. [9].

La figure 6 montre que l’utilisation des méthodes du gradient et de Lee et al. [31] amène à des valeurs de facteur de confinement, Cf, qui varient lorsque le rayon de contact évolue. On remarque aussi que Cf dépend du matériau ainsi que de son régime de déformation. Pour le matériau doux de la figure 5a, pour lequel le régime est purement plastique, Cf décroît avec 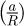, alors que pour le matériau dur de la figure 6b, qui se déforme dans un régime élasto-plastique, Cf augmente. Ces observations confirment les définitions des régimes de déformation proposées et les évolutions Cf constatées dans les travaux de Bartier et Hernot [38] et Bartier et al. [28].

Les conséquences des valeurs de Cf sur l’identification de la loi de comportement peuvent être remarquées dans la figure 7. Pour le cas du matériau doux, la sous-estimation de la valeur de Cf, obtenue avec la méthode de Tabor [7], a pour conséquence une surestimation des valeurs de contraintes représentatives par rapport à celles de la loi d’écrouissage solution. Pour Lee et al. [31], l’identification est évidemment correcte puisque le modèle d’application de la méthode utilise le modèle analytique de ces mêmes auteurs. On soulignera toutefois que les points identifiés se situent à des niveaux de déformation nettement supérieurs à ceux obtenus avec les autres méthodes, ce qui pourra amener à des problèmes d’identification dans le cas d’imprécision de mesures d’empreinte par exemple. Pour Ahn et Kwon [8], on rappelle que le facteur de confinement Cf a une valeur constante égale à 3 quel que soit le rayon de contact. Comme le montre la figure 6a, cette valeur est relativement proche de celles identifiées à partir de la méthode du gradient et du modèle de Lee et al. [31], dans le cas du matériau doux. En conséquence, l’identification avec ces méthodes amène à des valeurs de contraintes assez semblables. Toutefois, si l’on examine plus en détail les points identifiés de la loi d’écrouissage par la méthode d’Ahn et Kwon [8] ou Jeon et al. [9], on peut remarquer que ces points ont pour conséquence la prédiction d’un exposant d’écrouissage plus faible que celui du matériau « solution ».

Dans le cas du matériau dur, la figure 6b montre que la méthode de Tabor [7] a pour conséquence une surestimation du facteur de confinement pour les faibles rayons de contact et une sous-estimation de ce paramètre pour les plus grands rayons de contact. Comme le montre la figure 7b, la surestimation de Cf a pour conséquence la sous-estimation des valeurs de contraintes représentatives identifiées et la surestimation de Cf a pour conséquence la surestimation de ces valeurs. En ce qui concerne les méthodes de d’Ahn et Kwon [8] et Jeon et al. [17], la figure 7b montre que le facteur de confinement est surestimé. Cette surestimation a donc pour conséquence l’obtention de points représentatifs inférieurs à ceux de la courbe d’écrouissage « solution » (Fig. 7b).

Tableau 3

Proriétés mécanique des pseudo-matériaux doux et durs utilisés.

Mechanical properties of the soft and hard pseudo-materials.

thumbnail Fig. 5

Évolution des différentes déformations représentatives calculées en fonction du rapport (a/R) pour (a) un matériau doux et (b) un matériau dur.

Evolution of the different representative strains calculated as a function of the ratio (a/R) for (a) a soft material and (b) a hard material.
thumbnail Fig. 6

Évolution du facteur de confinement Cf en fonction du rapport (a/R) obtenue avec différentes méthodes pour (a) un matériau doux et (b) un matériau dur.

Evolution of the constraint factor Cf in function of the ratio (a/R) obtained with different methods for (a) a soft material and (b) a hard material.
thumbnail Fig. 7

Comparaison entre la courbe contrainte–déformation correspondant à la solution et les contraintes représentatives obtenues par indentation pour deux pseudo-matériaux : (a) matériau doux et (b) matériau dur.

Comparison between the stress–strain curve corresponding to the solution and the representative stresses obtained by indentation for two pseudo-materials: (a) soft material and (b) hard material.

5.3 Étude sur l’unicité de solution

Dans la partie précédente, le modèle d’application a été présenté pour un cas analytique ne présentant aucune incertitude ni erreur de mesure. Cependant, dans un cas expérimental, des incertitudes liées à des mesures expérimentales ou à des hétérogénéités du matériau peuvent survenir. Dans le cas de la mesure de dureté, l’erreur majeure peut venir de la mesure par microscope optique de la surface projetée de contact. Les empreintes n’ont pas toujours une forme géométrique parfaitement circulaire ce qui rend l’estimation du rayon de contact difficile (Fig. 8a). Cet aspect non circulaire peut être dû au comportement mécanique du matériau, comme c’est le cas, par exemple, pour le cuivre indenté qui ne se déforme pas de la même manière selon son orientation cristalline [39,40]. Il peut aussi être dû à la non-sphéricité de l’indenteur, notamment si le rayon de celui-ci est faible [39], ou encore à la présence de porosité, de rugosité, de contamination ou d’inclusions en surface du matériau [41–44]. La variation de dureté du matériau peut aussi tout simplement provenir de son hétérogénéité microstructurale [45].

Pour examiner l’influence de ces erreurs de mesures sur les résultats, le modèle analytique présenté précédemment a été reprogrammé pour prendre en compte des mesures erronées du rayon de l’empreinte a. Pour cette étude, un pseudo-matériau numérique, dont la loi d’écrouissage suit parfaitement la loi de Hollomon, est utilisé (E = 210 GPa, σy = 100 MPa, n = 0,3). En supposant une erreur de ± 10 % sur la mesure du diamètre de contact d, ce qui est une erreur importante comme le montre la figure 8b, 5 mesures erronées de la surface de contact sont considérées entre et .

La figure 9 présente les iso-valeurs de dureté obtenues pour différents rayons de contact adimensionnels lorsque l’on surestime de 10 % la valeur du diamètre de l’empreinte. Dans cette figure, on remarque que ces iso-valeurs de dureté ne s’interceptent pas en un seul point. Cinq iso-valeurs de dureté étant considérées, dix points d’intersection sont obtenus. Ceci indique que l’unicité de solution n’est pas garantie lorsque l’on identifie expérimentalement la loi d’écrouissage d’un matériau par indentation. À partir des dix points d’intersection, vingt valeurs de déformations représentatives et vingt valeurs de contraintes représentatives sont obtenues. En considérant une sous-estimation de 10 % de la valeur du diamètre de l’empreinte, dix autres points d’intersection entre les iso-valeurs de dureté et vingt autres couples εR − σR sont aussi obtenus. La figure 10 regroupe ces couples (εR − σR) et la courbe d’écrouissage correspondant à la solution (loi d’Hollomon avec E = 210 GPa, σy = 100 MPa, n = 0,3). Avec une surestimation de 10 % du diamètre de contact, la contrainte représentative est nettement sous-estimée, et inversement avec une sous-estimation de 10 % du diamètre de contact, la contrainte représentative est nettement surestimée.

thumbnail Fig. 8

Empreintes sur l’alliage d’aluminium AA2017. (a) Essai de micro-indentation avec une sphère de rayon 20 µm pour une charge 400 mN ; (b) Essai de macro-indentation avec une sphère de rayon 0,5 mm pour une charge 150 N.

Imprints on aluminium alloy AA2017. (a) Micro-indentation test with a sphere of radius 20 µm for a 400 mN load; (b) Macro-indentation test with a sphere of radius 0.5 mm for a 150 N load.
thumbnail Fig. 9

(a) Iso-valeurs de dureté obtenues dans l’espace [k, n] pour différents diamètres de contact surestimés de 10 %. (b) Zoom de la zone d’intersection des iso-valeurs de dureté.

(a) Hardness iso-values obtained in [k, n] space for different contact diameters overestimated by 10%. (b) Zoom of the intersection area of the hardness iso-values.
thumbnail Fig. 10

Comparaison entre la courbe contrainte–déformation correspondant à la solution (E = 210 GPa, σy = 100 MPa, n = 0,3) et les déformations et contraintes représentatives identifiées lorsqu’une erreur de ± 10 % sur la mesure du diamètre de contact est imposée.

Comparison between the stress-strain curve corresponding to the solution (E = 210 GPa, σy = 100 MPa, n = 0.3) and the representative strains and stresses identified when an error of ± 10% on the contact diameter measurement is imposed.

6 Application expérimentale

L’acier globulisé AISI 1035 est choisi pour tester la procédure d’identification proposée dans cet article. Ce type d’acier est sélectionné parce qu’il présente une microstructure fine et relativement homogène, ce qui permet d’obtenir une bonne reproductibilité des essais d’indentation. Les grains ferritiques et les anciens grains perlitiques dans lesquels les lamelles de cémentite ont été partiellement remplacées par des précipités de cémentite de forme sphéroïdale, peuvent être distingués sur la figure 11.

thumbnail Fig. 11

Microstructure de l’acier AISI 1035 globulisé après polissage mécanique et attaque au nital. Indication de la taille de l’empreinte obtenue avec un indenteur sphérique de rayon, R = 0,5 mm, et une charge appliquée de 15 N.

Microstructure of AISI 1035 globular steel after mechanical polishing and nital etching. Indication of the size of the indentation obtained with a spherical indenter of radius, R = 0.5 mm, and an applied load of 15 N.

6.1 Banc expérimental utilisé pour les essais d’indentation

Les essais expérimentaux d’indentation ont été réalisés en utilisant un banc instrumenté d’indentation conçu et réalisé au sein de notre laboratoire. Une cellule de charge mesure l’effort appliqué par l’indenteur avec une résolution de 0,02 N. Les essais ont été réalisés avec un indenteur sphérique de rayon R = 0,5 mm. La vitesse de déplacement a été imposée à environ 2 µm/s. Les essais d’indentation ont été réalisés sous diverses charges maximales de 15, 25, 50, 75, 150 et 200 N.

6.2 Détermination du rayon de contact

Le rayon d’empreinte a été déterminé par microscopie optique pour les différents essais d’indentation. Pour chaque empreinte, la valeur du rayon correspond à la moitié de la moyenne de 12 mesures de diamètre. Le rayon de contact à l'état de charge maximale est supposé être similaire au rayon de l'empreinte mesuré après le déchargement. Cette hypothèse est correcte si le déplacement radial du point situé au bord de l'empreinte du contact ne varie que très légèrement pendant le déchargement d’indentation, ce qui a été démontré numériquement dans une précédente étude [2].

6.3 Détermination de la loi d’écrouissage

Les 6 essais d’indentation effectués aboutissent à 6 valeurs de duretés. La figure 12 représente les iso-valeurs des différentes duretés identifiées dans l’espace [k, n]. Comme dans le cas où des erreurs auraient introduit numériquement sur le rayon de contact, l’essai expérimental conduit à différents points d’intersection des iso-valeurs de dureté. Tous ces points d’intersection peuvent être considérés comme points solutions pour l’identification des paramètres de loi d’écrouissage. Chaque point d’intersection de deux iso-valeurs de dureté donne deux valeurs de déformations représentatives par la méthode du gradient, ce qui conduit à trente valeurs différentes de déformations et contraintes représentatives.

Dans la figure 13a, l’évolution de la déformation représentative identifiée à partir de la méthode du gradient est comparée à celles obtenues par différents modèles de la littérature. Comme dans les cas numériques étudiés précédemment, la méthode du gradient proposée dans cet article conduit à des valeurs de déformation représentative situées entre celles proposées par Tabor [7] (Éq. (4)) et par Ahn et Kwon [8] (Éq. (5)). Les différentes méthodes étudiées conduisent à l’identification de contraintes représentatives assez proches de la courbe d’écrouissage « solution » obtenue par traction. Les points identifiés par la méthode du gradient conduit cependant aux points εR − σR les plus proches de la courbe « solution ». La méthode de Tabor [7] a tendance à caractériser un matériau plus résistant que celui caractérisé par traction et la méthode de Lee et al. [31] a tendance à caractériser un matériau moins écrouissable que celui caractérisé par traction.

thumbnail Fig. 12

Iso-valeurs de dureté dans l’espace [k, n] obtenues pour l’acier AISI 1035 globulisé avec différents rayons de contact.

Hardness iso-values in [k, n] space obtained for AISI 1035 steel and for different contact radius.
thumbnail Fig. 13

(a) Évolution des différentes déformations représentatives calculées en fonction du rapport (a/R) pour l’acier AISI 1035 ; (b) Comparaison entre la courbe contrainte-déformation solution obtenue par traction et les points représentatifs identifiés à partir des méthodes proposées pour le AISI 1035 globulisé.

(a) Evolution of the different representative strains calculated as a function of the ratio (a/R) for AISI 1035 steel; (b) Comparison of the stress-strain solution curve obtained from tensile test with the points identified from the methods proposed for AISI 1035.

7 Conclusion

Dans ce travail, différentes définitions de la déformation représentative basée sur la pression moyenne de contact sont présentées dans le cas de l’indentation sphérique.

Une nouvelle définition de la déformation représentative basée sur la pression moyenne de contact et valable pour une loi d’écrouissage de type Hollomon est ensuite proposée dans cet article. Contrairement aux autres méthodes basées sur la pression moyenne de contact proposée dans la littérature, cette nouvelle définition de déformation représentative n’est pas basée sur l’existence d’un facteur de confinement constant pour tous les matériaux indentés et pour tout régime de déformation. À partir de deux mesures de dureté obtenues pour deux efforts différents appliqués sur l’indenteur, la méthode appelée « méthode du gradient » permet à la fois d’identifier la limite d’élasticité, l’exposant d’écrouissage et deux déformations et contraintes représentatives de l’indentation. La déformation représentative identifiée dépend du gradient de dureté obtenue lorsque l’on fait varier les paramètres mécaniques du matériau autour de ceux préalablement identifiés. Pour montrer la validité de la méthode de détermination de la déformation représentative proposée, la méthode du gradient est appliquée à partir du modèle analytique proposé par Lee et al. [31]. Les résultats obtenus montrent que la déformation représentative identifiée augmente non linéairement lorsque le rayon de contact augmente, contrairement à ce que Tabor propose. Les valeurs de déformations et contraintes représentatives obtenues par la méthode proposée permettent de conclure qu’il n’existe pas de facteur de confinement universel constant indépendant du rapport adimensionnel et du matériau indenté. Le fait de ne pas imposer dans notre méthode de facteur de confinement constant a pour conséquence l’identification correcte de la loi d’écrouissage de matériaux doux ou durs, ce qui n’est pas le cas avec les différents modèles existants dans la littérature. Le travail présenté montre donc que la méthodologie d’identification basée sur un modèle de gradient de dureté et le modèle de Lee et al. [19] est pertinente pour obtenir la loi d’écrouissage de matériaux métalliques usuels (coefficient de Poisson proche de 0,3) dans le cas de conditions de frottement classiques (µ proche de 0,1).

Références

  1. J. Alcalá, A.C. Barone, M. Anglada, The influence of plastic hardening on surface deformation modes around Vickers and spherical indents, Acta Mater. 48(13), 3451–3464 (2000), https://doi.org/10.1016/S1359-6454(00)00140-3 [CrossRef] [Google Scholar]
  2. O. Bartier, X. Hernot, G. Mauvoisin, Theoretical and experimental analysis of contact radius for spherical indentation, Mech. Mater. 42(6), 640–656 (2010), https://doi.org/10.1016/j.mechmat.2010.03.003 [CrossRef] [Google Scholar]
  3. J.-M. Collin, G. Mauvoisin, R. El Abdi, An experimental method to determine the contact radius changes during a spherical instrumented indentation, Mech. Mater. 40(4), 401–406 (2008), https://doi.org/10.1016/j.mechmat.2007.10.002 [CrossRef] [Google Scholar]
  4. C. Schneider-Maunoury, A. Albayda, O. Bartier, On the use of instrumented indentation to characterize the mechanical properties of functionally graded binary alloys manufactured by additive manufacturing, Mater. Today Commun. 25, 101451 (2020), https://doi.org/10.1016/j.mtcomm.2020.101451 [CrossRef] [Google Scholar]
  5. C. Moussa, O. Bartier, X. Hernot, et al., Mechanical characterization of carbonitrided steel with spherical indentation using the average representative strain, Mater. Des. 89, 1191–1198 (2016), https://doi.org/10.1016/j.matdes.2015.10.067 [CrossRef] [Google Scholar]
  6. A. Nayebi, R. El Abdi, O. Bartier, et al., New procedure to determine steel mechanical parameters from the spherical indentation technique, Mech. Mater. 34(4), 243–254 (2002), https://doi.org/10.1016/S0167-6636(02)00113-8 [CrossRef] [Google Scholar]
  7. D. Tabor, The Hardness of Metals, Oxford University Press, Oxford, New York, 2000 [Google Scholar]
  8. J.-H. Ahn, D. Kwon, Derivation of plastic stress–strain relationship from ball indentations: Examination of strain definition and pileup effect, J. Mater. Res. 16(11), 3170–3178 (2001), https://doi.org/10.1557/JMR.2001.0437 [CrossRef] [Google Scholar]
  9. E. Jeon, M. Baik, S. Kim, et al., Determining representative stress and representative strain in deriving indentation flow curves based on finite element analysis, Key Eng. Mater. 297-300, 2152–2157 (2005), https://doi.org/10.4028/www.scientific.net/KEM.297-300.2152 [CrossRef] [Google Scholar]
  10. H. O’Neill, Hardness measurement of metals and alloys, 2nd ed., Springer, U.S., 1967, [online] https://www.springer.com/gp/book/9781504125215 (accessed 02/04/2021) [Google Scholar]
  11. W.C. Oliver, G.M. Pharr, An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments, J. Mater. Res. 7(6), 1564–1583 (1992), https://doi.org/10.1557/JMR.1992.1564 [CrossRef] [Google Scholar]
  12. B. Taljat, T. Zacharia, F. Kosel, New analytical procedure to determine stress–strain curve from spherical indentation data, Int. J. Solids Struct. 35(33), 4411–4426 (1998), https://doi.org/10.1016/S0020-7683(97)00249-7 [CrossRef] [Google Scholar]
  13. Y. Cao, J. Lu, A new method to extract the plastic properties of metal materials from an instrumented spherical indentation loading curve, Acta Mater. 52, 4023–4032 (2004), https://doi.org/10.1016/j.actamat.2004.05.018 [CrossRef] [Google Scholar]
  14. Y. Cao, X. Qian, N. Huber, Spherical indentation into elastoplastic materials: Indentation-response based definitions of the representative strain, Mater. Sci. Eng. A 454-455, 1–13 (2007), https://doi.org/10.1016/j.msea.2007.01.002 [CrossRef] [Google Scholar]
  15. M. Zhao, N. Ogasawara, N. Chiba, et al., A new approach to measure the elastic–plastic properties of bulk materials using spherical indentation, Acta Mater. 1(54), 23–32 (2006), https://doi.org/10.1016/j.actamat.2005.08.020 [CrossRef] [Google Scholar]
  16. N. Ogasawara, N. Chiba, X. Chen, A simple framework of spherical indentation for measuring elastoplastic properties, Mech. Mater. 41, 1025–1033 (2009), https://doi.org/10.1016/j.mechmat.2009.04.010 [CrossRef] [Google Scholar]
  17. E. Jeon, J.-Y. Kim, M.-K. Baik, et al., Optimum definition of true strain beneath a spherical indenter for deriving indentation flow curves, Mater. Sci. Eng. A 419(1), 196–201 (2006), https://doi.org/10.1016/j.msea.2005.12.012 [CrossRef] [Google Scholar]
  18. M.M. Chaudhri, Subsurface strain distribution around Vickers hardness indentations in annealed polycrystalline copper, Acta Mater. 46(9), 3047–3056 (1998), https://doi.org/10.1016/S1359-6454(98)00010-X [CrossRef] [Google Scholar]
  19. J.H. Lee, T. Kim, H. Lee, A study on robust indentation techniques to evaluate elastic–plastic properties of metals, Int. J. Solids Struct. 47(5), 647–664 (2010), https://doi.org/10.1016/j.ijsolstr.2009.11.003 [CrossRef] [Google Scholar]
  20. C. Yu, Y. Feng, R. Yang, et al., An integrated method to determine elastic–plastic parameters by instrumented spherical indentation, J. Mater. Res. 29(9), 1095–1103 (2014), https://doi.org/10.1557/jmr.2014.78 [CrossRef] [Google Scholar]
  21. L. Meng, B. Raghavan, O. Bartier, et al., An objective meta-modeling approach for indentation-based material characterization, Mech. Mater. 107, 31–44 (2017), https://doi.org/10.1016/j.mechmat.2017.01.011 [CrossRef] [Google Scholar]
  22. C. Moussa, X. Hernot, O. Bartier, et al., Evaluation of the tensile properties of a material through spherical indentation: definition of an average representative strain and a confidence domain, J. Mater. Sci. 2013, https://doi.org/10.1007/s10853-013-7739-1 [Google Scholar]
  23. M. Idriss, O. Bartier, G. Mauvoisin, et al., Determining the stress level of monotonic plastically pre-hardened metal sheets using the spherical instrumented indentation technique, J. Mech. Sci. Technol. 33, 183–195 (2019), https://doi.org/10.1007/s12206-018-1218-1 [CrossRef] [Google Scholar]
  24. P. Jiang, T. Zhang, R. Yang, Experimental verification for an instrumented spherical indentation technique in determining mechanical properties of metallic materials, J. Mater. Res. 26(11), 1414–1420 (2011), https://doi.org/10.1557/jmr.2011.51 [CrossRef] [Google Scholar]
  25. T. Zhang, S. Wang, W. Wang, Method to determine the optimal constitutive model from spherical indentation tests, Results Phys. 8, 716–727 (2018), https://doi.org/10.1016/j.rinp.2018.01.019 [CrossRef] [Google Scholar]
  26. L. Meng, P. Breitkopf, B. Raghavan, et al., On the study of mystical materials identified by indentation on power law and Voce hardening solids, Int. J. Mater. Form. 12(4), 587–602 (2019), https://doi.org/10.1007/s12289-018-1436-1 [CrossRef] [Google Scholar]
  27. M.M. Chaudhri, Subsurface plastic strain distribution around spherical indentations in metals, Philos. Mag. A 74(5), 1213–1224 (1996), https://doi.org/10.1080/01418619608239721 [Google Scholar]
  28. O. Bartier, X. Hernot, G. Mauvoisin, et al., Comparaison entre les déformations représentatives de l’indentation Vickers et de l’indentation sphérique, Matér. Tech. 101(3), Art. no. 3 (2013), https://doi.org/10.1051/mattech/2013072 [Google Scholar]
  29. X. Hernot, C. Moussa, O. Bartier, Study of the concept of representative strain and constraint factor introduced by Vickers indentation, Mech. Mater. 68, 1–14 (2014), https://doi.org/10.1016/j.mechmat.2013.07.004 [CrossRef] [Google Scholar]
  30. Abaqus documentation, https://abaqus-docs.mit.edu/2017/English/SIMACAEEXCRefMap/simaexc-c-docproc.htm (accessed 10/21/2021) [Google Scholar]
  31. H. Lee, J. Haeng Lee, G.M. Pharr A numerical approach to spherical indentation techniques for material property evaluation, J. Mech. Phys. Solids. 53(9), 2037–2069 (2005) https://doi.org/10.1016/j.jmps.2005.04.007 [CrossRef] [Google Scholar]
  32. J.R. Matthews, Indentation hardness and hot pressing, Acta Metall. 28(3), 311–318 (1980) [CrossRef] [Google Scholar]
  33. R. Hill, B. Storåkers, A.B. Zdunek, A theoretical study of the Brinell hardness test, Proc. R. Soc. Lond. Math. Phys. Sci. 423(1865), 301–330 (1989), https://doi.org/10.1098/rspa.1989.0056 [Google Scholar]
  34. X. Hernot, O. Bartier, Y. Bekouche, et al., Influence of penetration depth and mechanical properties on contact radius determination for spherical indentation, Int. J. Solids Struct. 43(14-15), 4136–4153 (2006), https://doi.org/10.1016/j.ijsolstr.2005.06.007 [CrossRef] [Google Scholar]
  35. S.H. Kim, B.W. Lee, Y. Choi, et al., Quantitative determination of contact depth during spherical indentation of metallic materials – A FEM study, Mater. Sci. Eng. A 1-2(415), 59–65 (2006), https://doi.org/10.1016/j.msea.2005.08.217 [CrossRef] [Google Scholar]
  36. M. Kim, K.P. Marimuthu, J.H. Lee, et al., Spherical indentation method to evaluate material properties of high-strength materials, Int. J. Mech. Sci. 106, 117–127 (2016), https://doi.org/10.1016/j.ijmecsci.2015.12.008 [CrossRef] [Google Scholar]
  37. Python Release Python 3.3.0, Python.org., https://www.python.org/downloads/release/python-330/ (accessed 10/21/2021) [Google Scholar]
  38. O. Bartier, X. Hernot, Phenomenological study of parabolic and spherical indentation of elastic-ideally plastic material, Int. J. Solids Struct. 49, 2015–2026 (2012), https://doi.org/10.1016/j.ijsolstr.2012.04.005 [CrossRef] [Google Scholar]
  39. Y.Y. Lim, M.M. Chaudhri, Indentation of rigid cones into conical holes molded in elastic blocks, J. Appl. Phys. 98(7), 073518 (2005), https://doi.org/10.1063/1.2060933 [CrossRef] [Google Scholar]
  40. A.J. Cackett, C.D. Hardie, J.J.H. Lim, et al., Spherical indentation of copper: Crystal plasticity vs. experiment, Materialia 7, 100368 (2019), https://doi.org/10.1016/j.mtla.2019.100368 [CrossRef] [Google Scholar]
  41. J.J. Roa, E. Jiménez-Piqué, X.G. Capdevila, et al., Nanoindentation with spherical tips of single crystals of YBCO textured by the Bridgman technique: Determination of indentation stress–strain curves, J. Eur. Ceram. Soc. 30(6), 1477–1482 (2010), https://doi.org/10.1016/j.jeurceramsoc.2009.10.021 [CrossRef] [Google Scholar]
  42. L. Chen, A. Ahadi, J. Zhou, et al., Numerical and experimental study of the roughness effects on mechanical properties of AISI316L by nanoindentation, Model. Numer. Simul. Mater. Sci. 4(4), Art. no. 4 (2014), https://doi.org/10.4236/mnsms.2014.44017 [Google Scholar]
  43. D. Chicot, H. Ageorges, M. Voda, Hardness of thermal sprayed coatings: Relevance of the scale of measurement, Surf. Coat. Technol. 268, 173–179 (2015), https://doi.org/10.1016/j.surfcoat.2014.04.043 [CrossRef] [Google Scholar]
  44. O. Iracheta, C.J. Bennett, W. Sun, The influence of the indentation size in relation to the size of the microstructure of three polycrystalline materials indented with a Berkovich indenter, Mater. Sci. Eng. A., (2017), https://doi.org/10.1016/j.msea.2017.08.023 [Google Scholar]
  45. D.M. De Bono, T. London, M. Baker, et al., A robust inverse analysis method to estimate the local tensile properties of heterogeneous materials from nano-indentation data, Int. J. Mech. Sci. 123, 162–176 (2017), https://doi.org/10.1016/j.ijmecsci.2017.02.006 [CrossRef] [Google Scholar]

Citation de l’article : Alaa Albayda, Olivier Bartier, Xavier Hernot, Gérard Mauvoisin, Identification de la déformation représentative et de la loi d’écrouissage des matériaux avec l’indentation sphérique en se basant sur un modèle de gradient de dureté, Matériaux & Techniques 110, 205 (2022)

Liste des tableaux

Tableau 1

Propriétés mécaniques du pseudo-matériau utilisé pour montrer le signal bruité du gradient de dureté obtenu par élément finis.

Mechanical properties of the pseudo-material used to show the noisy signal of the hardness gradient obtained by finite element.

Dans le texte
Tableau 2

Valeurs des paramètres mécaniques de matériaux indentés utilisés pour la détermination du modèle proposé par Lee et al. [31].

Values of mechanical parameters of indented materials used for determination of the model proposed by Lee et al. [31].

Dans le texte
Tableau 3

Proriétés mécanique des pseudo-matériaux doux et durs utilisés.

Mechanical properties of the soft and hard pseudo-materials.

Dans le texte

Liste des figures

thumbnail Fig. 1

Modèle EF axisymétrique pour une indentation sphérique avec des éléments CAX4.

Axisymmetric FE model for spherical indentation with CAX4 elements.
Dans le texte
thumbnail Fig. 2

Évolution bruitée de la déformation représentative en fonction du rayon de contact adimensionnel (a/R) obtenue par simulation EF à partir de la méthode du gradient de dureté pour une perturbation de ± 2,16 % pour k et ± 2,16 % pour n.

Noise evolution of the representative strain as a function of the dimensionless contact radius (a/R) obtained by FE simulation from the hardness gradient method for a perturbation of ± 2.16% for k and ± 2.16% for n.
Dans le texte
thumbnail Fig. 3

Comparaison entre les efforts obtenus pour deux rayons de contact (0,2 R et 0,3 R) avec le modèle analytique de Lee et al. [31] programmé sous Python et la courbe F(a) obtenue par EF (pseudo matériau : E = 210 GPa, σy = 100 MPa, n = 0,3).

Comparison between the forces obtained for two contact radius (0.2 R and 0.3 R) with the analytical model of Lee et al. [31] programmed in Python and the F(a) curve obtained by FE (pseudo material: E = 210 GPa, σy = 100 MPa, n = 0.3).
Dans le texte
thumbnail Fig. 4

Iso-valeurs de dureté obtenues pour deux rayons de contact égal à 0,2 R et 0,3 R. (a) Représentation dans l’espace [σy, n] ; (b) Représentation dans l’espace [k, n].

Hardness iso-values obtained for two contact radii equal to 0.2 R and 0.3 R. (a) Representation in [σy, n] space; (b) Representation in [k, n] space.
Dans le texte
thumbnail Fig. 5

Évolution des différentes déformations représentatives calculées en fonction du rapport (a/R) pour (a) un matériau doux et (b) un matériau dur.

Evolution of the different representative strains calculated as a function of the ratio (a/R) for (a) a soft material and (b) a hard material.
Dans le texte
thumbnail Fig. 6

Évolution du facteur de confinement Cf en fonction du rapport (a/R) obtenue avec différentes méthodes pour (a) un matériau doux et (b) un matériau dur.

Evolution of the constraint factor Cf in function of the ratio (a/R) obtained with different methods for (a) a soft material and (b) a hard material.
Dans le texte
thumbnail Fig. 7

Comparaison entre la courbe contrainte–déformation correspondant à la solution et les contraintes représentatives obtenues par indentation pour deux pseudo-matériaux : (a) matériau doux et (b) matériau dur.

Comparison between the stress–strain curve corresponding to the solution and the representative stresses obtained by indentation for two pseudo-materials: (a) soft material and (b) hard material.
Dans le texte
thumbnail Fig. 8

Empreintes sur l’alliage d’aluminium AA2017. (a) Essai de micro-indentation avec une sphère de rayon 20 µm pour une charge 400 mN ; (b) Essai de macro-indentation avec une sphère de rayon 0,5 mm pour une charge 150 N.

Imprints on aluminium alloy AA2017. (a) Micro-indentation test with a sphere of radius 20 µm for a 400 mN load; (b) Macro-indentation test with a sphere of radius 0.5 mm for a 150 N load.
Dans le texte
thumbnail Fig. 9

(a) Iso-valeurs de dureté obtenues dans l’espace [k, n] pour différents diamètres de contact surestimés de 10 %. (b) Zoom de la zone d’intersection des iso-valeurs de dureté.

(a) Hardness iso-values obtained in [k, n] space for different contact diameters overestimated by 10%. (b) Zoom of the intersection area of the hardness iso-values.
Dans le texte
thumbnail Fig. 10

Comparaison entre la courbe contrainte–déformation correspondant à la solution (E = 210 GPa, σy = 100 MPa, n = 0,3) et les déformations et contraintes représentatives identifiées lorsqu’une erreur de ± 10 % sur la mesure du diamètre de contact est imposée.

Comparison between the stress-strain curve corresponding to the solution (E = 210 GPa, σy = 100 MPa, n = 0.3) and the representative strains and stresses identified when an error of ± 10% on the contact diameter measurement is imposed.
Dans le texte
thumbnail Fig. 11

Microstructure de l’acier AISI 1035 globulisé après polissage mécanique et attaque au nital. Indication de la taille de l’empreinte obtenue avec un indenteur sphérique de rayon, R = 0,5 mm, et une charge appliquée de 15 N.

Microstructure of AISI 1035 globular steel after mechanical polishing and nital etching. Indication of the size of the indentation obtained with a spherical indenter of radius, R = 0.5 mm, and an applied load of 15 N.
Dans le texte
thumbnail Fig. 12

Iso-valeurs de dureté dans l’espace [k, n] obtenues pour l’acier AISI 1035 globulisé avec différents rayons de contact.

Hardness iso-values in [k, n] space obtained for AISI 1035 steel and for different contact radius.
Dans le texte
thumbnail Fig. 13

(a) Évolution des différentes déformations représentatives calculées en fonction du rapport (a/R) pour l’acier AISI 1035 ; (b) Comparaison entre la courbe contrainte-déformation solution obtenue par traction et les points représentatifs identifiés à partir des méthodes proposées pour le AISI 1035 globulisé.

(a) Evolution of the different representative strains calculated as a function of the ratio (a/R) for AISI 1035 steel; (b) Comparison of the stress-strain solution curve obtained from tensile test with the points identified from the methods proposed for AISI 1035.
Dans le texte

Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.

Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.

Le chargement des statistiques peut être long.