| Numéro |
Matériaux & Techniques
Volume 106, Numéro 3, 2018
Assemblages Mécaniques / Mechanical Assemblies
|
|
|---|---|---|
| Numéro d'article | 302 | |
| Nombre de pages | 10 | |
| Section | Assemblage / Joining and assembly | |
| DOI | https://doi.org/10.1051/mattech/2018052 | |
| Publié en ligne | 23 novembre 2018 | |
Regular Article
Détermination de la souplesse hors plan d’un assemblage de composites boulonnés à l’aide d’une démarche d’homogénéisation
Determination of the out-of-plane flexibility of a bolted composite assembly using a homogenization approach
1
GeM, École Centrale de Nantes, Université de Nantes, UMR CNRS 6183,
1 rue de la Noé,
44321
Nantes Cedex 3, France
2
CETIM, Pôle IDA – Ingénierie des Assemblages,
74 route de la Jonelière,
44326
Nantes Cedex 3, France
3
CETIM, Pôle IDA– Ingénierie des Assemblages,
7 rue de la Presse,
42952
Saint-Étienne, France
* e-mail: laurent.gornet@ec-nantes.fr
** e-mail: frederic.jacquemin@univ-nantes.fr
Reçu :
15
Octobre
2017
Accepté :
1
Octobre
2018
Dans de nombreux secteurs industriels, les matériaux composites tissés à fibres de carbone et matrices thermoplastiques semblent être une alternative prometteuse aux matériaux métalliques pour alléger les structures. Les matrices composites thermoplastiques ont un coût plus adapté à la fabrication de pièces composites avec de grandes cadences. Les assemblages de structures peuvent être des jonctions mécaniques à base de rivets, de vis ou de boulons. Dans cette étude, nous proposons de développer une approche expérimentale et numérique pour identifier les souplesses hors plan des constituants élémentaires d’un assemblage boulonné. Il n’y a actuellement aucune règle de conception pour prédire la rupture des liaisons boulonnées constituées de substrats composites thermoplastiques. Par conséquent, une étude expérimentale d’une liaison boulonnée utilisant la technique de corrélation d’images est présentée. Simultanément, des modèles éléments finis tridimensionnels d’assemblages associés à une approche d’équivalence en énergie ont été développés afin de déterminer la souplesse des éléments de l’assemblage. Ces modèles éléments finis ont ensuite été comparés avec succès à des résultats expérimentaux.
Abstract
Woven carbon fiber-thermoplastic matrix composite materials appear to be a promising alternative to metallic materials by lightening structures in many industrial sectors. Moreover, composite thermoplastic matrices have a more adapted cost to the manufacture of parts with large throughput. The assemblies of structures can be mechanical junctions based on rivets, screws or bolts. In this study, we propose to develop an experimental and numerical approach to identify the out-of-plane flexibility of the bolted assembly elementary constituents. There are currently no design rules for predicting fracture of bolted-based thermoplastic composite substrates bonds. Therefore, an experimental study of the bolted connection using the image correlation technique is presented. At the same time, three-dimensional finite element assembly models associated with an energy equivalence approach have been developed in order to simulate the flexibility of the assembly parts. These finite element models were then successfully compared to experimental results.
Mots clés : assemblage boulonnés / composite thermoplastique / souplesse / homogénéisation
Key words: bolted assembly / thermoplastic composite / flexibility / homogenization
© EDP Sciences, 2018
1 Introduction
De nos jours, les matériaux composites tissés à renforts carbone et résine thermoplastique sont utilisés dans différents domaines industriels, notamment, dans la construction automobile et aéronautique. Les outils traditionnels de dimensionnement des assemblages boulonnés de pièces métalliques sont basés sur la norme NF E 25-030-1, NF E 25-030-2 [1–2] ou sur la recommandation VDI2230 [3] établie par Verein Deutscher Ingenieure. Ces travaux constituent le socle du logiciel Cobra V6 développé par le CETIM. La recommandation VDI 2230 est destinée à modéliser les souplesses hors plan des assemblages métalliques. Elle est constituée de modèles analytiques dont les hypothèses doivent être revisitées dans le cas de l’assemblage de matériaux composites. L’objet de cette étude est d’améliorer la compréhension de la VDI 2230 et par conséquence la modélisation des souplesses utilisées pour le dimensionnement des assemblages boulonnés [3]. L’objectif de nos travaux est de développer une approche permettant de déterminer les souplesses de substrats composites orthotropes carbone/thermoplastique. Nous proposons une démarche expérimentale et numérique destinée à déterminer les souplesses hors plan des différents éléments d’un assemblage boulonné. Les développements ont été réalisés avec le code éléments finis Cast3M développé par le CEA. Le critère énergétique proposé permet de retrouver le comportement hors plan des zones d’assemblages boulonnés modélisées traditionnellement par des cônes de Rötscher [4] dans la VDI 2230. Le modèle dédié aux assemblages métalliques proposé par Rötscher fait l’hypothèse que la force sous la tête de la vis se répartit dans les plaques sous forme d’un cône tronqué creux à 45° suivi d’un cône tronqué creux à 45° inversé (Fig. 1). Des essais mécaniques ont été réalisés afin de déterminer les souplesses et le coefficient de filtrage d’un assemblage boulonné. Le comportement mécanique élastique tridimensionnel du volume élémentaire représentatif du composite est reconstruit par une procédure d’homogénéisation. Par la suite, une démarche d’homogénéisation est proposée pour modéliser les souplesses d’un assemblage. Elle permet de retrouver les valeurs des souplesses des éléments mécaniques de la zone assemblée constituée de matériaux métalliques. Les résultats obtenus sont équivalents à ceux proposés par le logiciel Cobra dont les fondements théoriques sont issus de la VDI 2230. La méthode numérique proposée ne comporte pas d’hypothèses restrictives sur le comportement élastique des constituants. Cette méthode est utilisée avec succès dans le cas du boulonnage de tissus composites orthotropes. Enfin, il convient de noter que la spécificité liée aux assemblages de matériaux composites thermoplastiques est la reprise en humidité ou le fluage qui doivent à terme être inclus dans l’approche proposée.
 |
Fig. 1 Assemblage de deux pièces mécaniques par une liaison boulonnée. L’effort exercé par le boulon est repris dans les deux pièces par des zones tronc coniques creuses à 45° (cônes de Rötscher). Assembly of two mechanical parts by a bolted connection. The force exerted by the bolt is taken up in both parts by 45° hollow conical trunks (Rötscher cones). |
2 Caractérisation du composite thermoplastique T700/PA66
L’identification du comportement mécanique d’un matériau composite tissé nécessite de réaliser des essais sur une base canonique d’éprouvettes. Cette base est constituée d’éprouvettes sens chaîne [0°], sens trame [90°] et de cisaillement plan [± 45°]. Les orientations des directions d’orthotropie (chaîne et trame) sont exprimées par rapport au repère global de l’éprouvette (Fig. 2). Le comportement mécanique élastique dans le plan d’un tissu équilibré peut être obtenu uniquement à partir de deux types d’essais de traction (sens chaîne, cisaillement plan). Cette approche simplifiée permet de réduire le nombre d’éprouvettes à tester. Le module de Young hors plan du composite est un paramètre du premier ordre dans le cas d’un assemblage. Il a été obtenu à l’aide d’essais de compression hors plan. Enfin, l’ensemble des propriétés mécaniques élastiques peut être reconstruit à partir d’une procédure d’homogénéisation du Volume Élémentaire Représentatif du composite. L’objectif ultime est d’utiliser l’ensemble des caractéristiques obtenues afin de mener des simulations numériques des pertes de serrage d’un assemblage boulonné constitué de matériaux composites. Les phénomènes de viscosité et d’endommagement lors de charge et décharges déjà modélisés dans le plan par un modèle à dérivées fractionnaire sont responsables des pertes de serrage [5–6]. La prise en compte des propriétés mécaniques réalistes du stratifié T700/PA66 permettra ainsi d’améliorer la modélisation de la tenue d’un assemblage boulonné précontraint (Tab. 1).
 |
Fig. 2 Dimensions nominales des éprouvettes en mm. Nominal specimen dimensions in mm. |
Propriétés élastiques du tissu équilibré T700/PA66.
Elastic properties of the balanced fabric T700/PA66.
2.1 Essais dans le plan du tissu stratifié
Les essais quasi-statiques permettent de déterminer les caractéristiques mécaniques initiales du tissu sergé équilibré T700/PA66 ainsi que leurs évolutions en fonction du temps. Ces essais ont été réalisés sur une machine à mors hydraulique MTS d’une capacité de 10 tonnes du laboratoire GeM. Le pilotage des essais s’effectue à déplacement imposé et à une vitesse de chargement de 2,4 mm/min. Les mesures des déformations dans le plan sont réalisées par une méthode classique, via des jauges de déformation bidirectionnelles (Fig. 2). L’enregistrement des données est réalisé à partir d’une électronique de mesure QuantumX HBM associé au logiciel Catman®. L’identification du comportement mécanique du matériau impose la réalisation d’essais quasi-statiques sur une base canonique d’éprouvettes permettant de caractériser les réponses du matériau dans les sens trame, chaîne et en cisaillement plan. Les essais de traction réalisés avec des charges et des décharges afin d’évaluer les propriétés d’endommagement et de déformations irréversibles sont présentés dans les figures 3 et 4.
 |
Fig. 3 Comportement dans le sens chaîne [0°]. Behaviour in the chain direction [0°]. |
 |
Fig. 4 Comportement en cisaillement plan [± 45°]. Évolution des modules sécants. Plane shear behaviour [± 45°]. Evolution of secant modules. |
2.2 Essais hors plan
Le comportement mécanique hors plan d’un assemblage boulonné constitué de plaques composites, ou plus généralement de plaques composées d’un multi-matériau [7], influence fortement l’étendue des contraintes vues par le boulon [8]. Un point clef du dimensionnement des assemblages boulonnés consiste à déterminer avec précision la souplesse en compression hors plan de l’assemblage, elle-même dépendante des modules plan et hors plan des stratifiés en présence. Les échantillons destinés à caractériser le module hors plan E3 sont des parallélépipèdes de 30 × 40 mm2. Différentes épaisseurs ont été testées en collant plusieurs plaques élémentaires de T700/PA66. Le comportement viscoélastique peut être influencé par la présence d’une fine couche de colle permettant l’adhésion des plaques. La souplesse de chaque joint de colle est considérée négligeable, compte-tenu de sa faible épaisseur au regard de celle du composite (50 μm de colle pour 2 mm de stratifié). Les essais de compression ont été réalisés sur une machine Instron 5584 équipée de plateaux rotulés. La mesure de déplacement est effectuée par corrélation d’images au moyen d’une caméra STEMMER GT6600 (capteur CCD à 29 mégapixels KAI-29050 de Truesense Imaging) et du logiciel d’acquisition VIC Snap. L’exploitation est réalisée avec le logiciel VIC 2D. Les atouts de cette méthode sont la rapidité de la mesure, la précision, la sensibilité et une grande résolution spatiale. Celle-ci autorise également des chargements rapides. Diverses épaisseurs ont été testées afin d’évaluer l’impact sur la valeur du module hors plan E3. Les résultats, présentés dans le tableau 2, concernent les modules hors plan pour des stratifiés de 16 mm et 32 mm d’épaisseur. Les essais ont été réalisés pour trois éprouvettes et chaque essai a été répété trois fois, les moyennes sont données dans le tableau 2. Ces essais de compression hors plan ont révélé des valeurs du module E3 comprise entre 4931 et 5918 MPa selon les échantillons. La littérature mentionne des valeurs de 1700 à 2000 MPa à Tamb pour la résine PA66 (HR 50) seule. Par la suite, le module hors plan est déterminé à l’aide d’une procédure d’homogénéisation périodique permettant d’obtenir des modules plans conformes aux essais réalisés pour une seule couche de matériau. La variabilité hors plan des propriétés du matériau en fonction de l’épaisseur est due au positionnement irrégulier dans le plan des Volumes Élémentaires Représentatifs des tissus élémentaires superposés.
Valeurs expérimentales du module hors plan du T700/PA66 en fonction de son épaisseur.
Experimental values of the out-of-plane module of the T700/PA66 as a function of its thickness.
2.3 Modélisation tridimensionnelle du comportement mécanique élastique orthotrope
L’objectif de cette partie est de déterminer numériquement le comportement mécanique élastique tridimensionnel du VER de tissu composite T700/PA66. Les relations de comportement entre les contraintes moyennes Σ et les déformations moyennes E du V.E.R. sont notées respectivement en souplesse SVER et en complaisance CVER. La relation de comportement en notation de Voigt est : E = SVER Σ avec SVER = CVER−1. La méthode d’homogénéisation périodique retenue est fondée sur la donnée du champ de déformation moyenne E du VER et conduit à déterminer l’opérateur de complaisance du VER CVER à partir de conditions limites en déplacements imposés sur son bord. Le processus d’homogénéisation retenu est basé sur la résolution de 6 problèmes d’élasticité linéaire élémentaires posés sur le VER (Éq. (1)). Ces six problèmes d’élasticité linéaire à résoudre correspondent aux 6 déformations macroscopiques E. La détermination de la rigidité du VER nécessite quant à elle 21 combinaisons linéaires des six problèmes élémentaires dans le cas général. Les problèmes élémentaires à résoudre sur le VER sont présentés ci-après :
 (1)
(1)
Le champ de déplacement 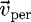 est périodique et prend naturellement des valeurs égales sur les faces opposées du VER (Fig. 5). Des relations linéaires peuvent être écrites entre deux faces opposées du VER pour éliminer le champ périodique. Les caractéristiques mécaniques homogénéisées du VER peuvent être déterminées simplement par l’approche énergétique qui est fondée sur le théorème de Hill-Mandel. Le théorème impose que l’énergie du VER est la moyenne de l’énergie de ces constituants élémentaires. Le théorème est noté : Σ : E =⟨ σϵ ⟩. En prenant en compte le comportement en rigidité du VER on obtient (Éq. (2)) :
est périodique et prend naturellement des valeurs égales sur les faces opposées du VER (Fig. 5). Des relations linéaires peuvent être écrites entre deux faces opposées du VER pour éliminer le champ périodique. Les caractéristiques mécaniques homogénéisées du VER peuvent être déterminées simplement par l’approche énergétique qui est fondée sur le théorème de Hill-Mandel. Le théorème impose que l’énergie du VER est la moyenne de l’énergie de ces constituants élémentaires. Le théorème est noté : Σ : E =⟨ σϵ ⟩. En prenant en compte le comportement en rigidité du VER on obtient (Éq. (2)) :
 (2)
(2)
L’approche précédente définit le comportement homogénéisé sous forme d’une loi élastique linéaire anisotrope que l’on détermine en résolvant les six problèmes élémentaires posés sur le VER. La loi de comportement en souplesse du matériau homogène équivalent est déterminée à partir de l’inversion de la matrice 6 * 6 contenant les rigidités déterminées par le théorème d’équivalence en énergie de Hill Mandel : SVER = CVER−1. Dans le cas des milieux périodiques, l’approche en contraintes imposées et l’approche en déformations sont équivalentes [7].
Les modules (E3,G12,G13,G23) sont fortement influencés par le comportement mécanique de la matrice PA66. En conséquence, ces modules peuvent varier de manière non négligeable en fonction de la température et de l’humidité ambiante. Classiquement, les matériaux sont testés à température ambiante pour une humidité relative de 50 % (HR 50). Ces paramètres environnementaux agissent sur la valeur de la température de transition vitreuse du matériau qui gouverne directement l’évolution de ces modules. Le comportement élastique orthotrope tridimensionnel est construit à partir d’une procédure d’homogénéisation et d’une analyse inverse associée aux essais mécaniques réalisés. Le motif géométrique élémentaire du Volume Élémentaire Représentatif du tissu T700/PA66 est composé de 4 torons de fibres dans le sens chaîne et 4 torons de fibres dans le sens trame (Fig. 5). Les simulations ont été réalisées à l’aide d’un programme développé au laboratoire sur la base du code éléments finis Cast3M. Le comportement d’un toron de fibres (Fig. 5) est supposé élastique isotrope transverse (Tab. 3). Le pourcentage de la matrice dans le toron de fibres peut atteindre 25 %. Le comportement hors plan du matériau est fortement influencé par le module transverse du toron. Les propriétés du toron de fibre retenu sont présentées dans le tableau 3. Le comportement de la matrice est isotrope (Em = 2730 GPa, vm = 0,3). Le calcul montre bien que la réponse du module hors plan est pilotée par la réponse hors plan du Toron T700/Pa66. Dans le cas présenté, un toron de module transverse E3 de 7000 MPa (Tab. 3) conduit à une propriété homogénéisée du tissu E3 de 6474 MPa (Tab. 4).
Les propriétés mécaniques élastiques orthotropes du stratifié T700/PA66, basées sur les essais et la procédure d’homogénéisation par éléments finis, sont présentées dans le tableau 4.
 |
Fig. 5 Volume Élémentaire Représentatif du Tissu T700/Pa66 voxélisé utilisé pour l’homogénéisation. Representative Elementary Volume of the T700/Pa66 voxelized fabric used for homogenization. |
Propriétés élastiques du toron de fibres T700/PA66 utilisé dans les simulations EF.
Elastic properties of the fibers’ strand T700/PA66 used in finite element simulations.
Propriétés élastiques homogénéisées du tissu T700/PA66.
Homogenized elastic properties of the T700/PA66 fabric.
3 Assemblages boulonnés composites thermoplastiques
L’objectif est de valider les souplesses des liaisons boulonnées précontraintes à base de substrats en composite T700/PA66. La VDI 2230 montre qu’une précontrainte axiale maîtrisée dans la vis permet de filtrer les sollicitations dynamiques vues par la fixation, et donc d’améliorer très sensiblement sa durée de vie dans le cas d’assemblage métallique. Cette norme est limitée aux matériaux isotropes. L’objectif de cette partie est de proposer une démarche d’homogénéisation permettant de caractériser les souplesses d’une liaison boulonnée constituée de plaques composites orthotropes. Cette approche est mise en œuvre avec le code éléments finis Cast3M. Nous montrons que l’approche proposée permet de retrouver les résultats fournis par la VDI 2230 dans le cas des assemblages boulonnés métalliques (Logiciel Cobra). Dans le cas des matériaux métalliques la forme de reprise des efforts cône tronqué creux est retrouvée. La méthode numérique d’homogénéisation proposée est ensuite appliquée à un assemblage de deux plaques stratifiées orthotropes T700/PA66.
3.1 Détermination des souplesses élémentaires de l’assemblage par un critère énergétique
Nous proposons de déterminer les souplesses élémentaires des éléments de l’assemblage (Fig. 1) à l’aide d’une procédure d’homogénéisation. Les souplesses élémentaires de l’assemblage sont notées respectivement pour le boulon et les deux pièces 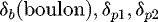 . Ce travail se base sur les idées développées dans la VDI 2230 où la souplesse des éléments de l’assemblage δ est modélisée par trois barres élémentaires (boulon, pièce 1 et pièce 2). La démarche proposée permet de déterminer les souplesses élémentaires par une équivalence énergétique entre la liaison boulonnée élastique tridimensionnelle modélisée par éléments finis (Fig. 1) et un milieu unidimensionnel homogénéisé équivalent de souplesseδ.
. Ce travail se base sur les idées développées dans la VDI 2230 où la souplesse des éléments de l’assemblage δ est modélisée par trois barres élémentaires (boulon, pièce 1 et pièce 2). La démarche proposée permet de déterminer les souplesses élémentaires par une équivalence énergétique entre la liaison boulonnée élastique tridimensionnelle modélisée par éléments finis (Fig. 1) et un milieu unidimensionnel homogénéisé équivalent de souplesseδ.
L’approximation géométrique du domaine de reprise des efforts de serrage de forme cône tronqué creux admise pour les matériaux métalliques n’est pas appropriée pour les matériaux composites de nature orthotrope. Afin de lever cette hypothèse géométrique, nous proposons d’utiliser l’iso valeur zéro de l’énergie de déformation réduite à sa composante hors plan ( ) pour définir le volume tridimensionnel qui supporte les efforts de serrage Vr. Dans le cas des matériaux métallique la zone Vr dans les plaques a la forme de cônes tronqués creux (VDI 2230). La démarche d’homogénéisation proposée est basée sur l’équivalence énergétique entre les efforts externes et internes du problème considéré, posée sur le volume total Vr ∪ Vbr. Le volume Vbr ne participe pas à la reprise des efforts d’un point de vue énergétique. L’approche proposée sur un domaine élastique se traduit par la formule suivante :
) pour définir le volume tridimensionnel qui supporte les efforts de serrage Vr. Dans le cas des matériaux métallique la zone Vr dans les plaques a la forme de cônes tronqués creux (VDI 2230). La démarche d’homogénéisation proposée est basée sur l’équivalence énergétique entre les efforts externes et internes du problème considéré, posée sur le volume total Vr ∪ Vbr. Le volume Vbr ne participe pas à la reprise des efforts d’un point de vue énergétique. L’approche proposée sur un domaine élastique se traduit par la formule suivante :
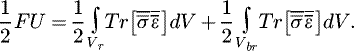 (3)
(3)
La souplesse du système est définie par la relation 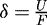 (notation de la norme VDI).
(notation de la norme VDI).
Où U et F représente, respectivement, le déplacement et l’effort du domaine équivalent. Dès lors que l’énergie de déformation ne passe que dans la partie Vr, nous pouvons écrire que la souplesse de l’assemblage s’écrit à partir de la relation :
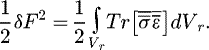 (4)
(4)
La souplesse de l’assemblage peut s’exprimer en fonction de l’énergie de déformation comprise dans la zone géométrique Vr de reprise des efforts d’assemblage comme suit :
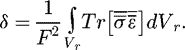 (5)
(5)
Cette démarche énergétique peut être écrite pour les différents constituants de l’assemblage. Dans ce cas, la force F correspond à la résultante des efforts de pression de serrage due à la précontrainte engendrée par le boulon sur les plaques assemblées et U correspond au déplacement associé. Dans le cas d’un assemblage constitué d’un boulon (indice b) et de deux pièces (indices p1 et p2), cette expression devient :
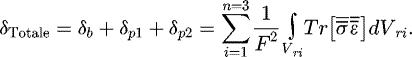 (6)
(6)
La modélisation des souplesses par un assemblage de barres en serie est communément admise dans la norme [1–2]. Il convient de noter que dans le cas particulier d’un assemblage centré, sollicité axialement, l’énergie de déformation volumique peut être approximée comme 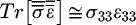 . Dans le cas d’une liaison boulonnée travaillant en flexion, la zone de souplesse de reprise d’effort et le boulon doivent être homogénéisés avec une hypothèse cinématique de poutre et non de barre [1–3]. Dans le cas de matériaux homogènes et isotropes, cette approche énergétique permet de déterminer des souplesses équivalentes à celles obtenues analytiquement d’après la formulation VDI. Le logiciel Cobra V6 développé par le CETIM est basé sur les formules VDI 2230. Les comparaisons entre les résultats issus de notre méthode d’homogénéisation et Cobra V6 sont présentées pour un assemblage boulonné constitué de deux plaques circulaires d’aluminium 7075T6 (Tab. 5). Les simulations éléments finis ont été menées en axisymétrique à l’aide du code Cast3M. La figure 6 représente l’évolution des souplesses de la zone assemblée en fonction des diamètres des plaques Dp. La figure 7 représente pour les mêmes conditions de serrage l’évolution de la souplesse du boulon. Il convient de noter que l’approche numérique développée ne fait aucune hypothèse sur l’isotropie du matériau. En conséquence, la démarche proposée est applicable pour un assemblage de matériaux composite à comportement élastique orthotrope [9]. La souplesse calculée par éléments finis peut être identifiée à un modèle de barre ou de poutre comme préconisé dans [1–3].
. Dans le cas d’une liaison boulonnée travaillant en flexion, la zone de souplesse de reprise d’effort et le boulon doivent être homogénéisés avec une hypothèse cinématique de poutre et non de barre [1–3]. Dans le cas de matériaux homogènes et isotropes, cette approche énergétique permet de déterminer des souplesses équivalentes à celles obtenues analytiquement d’après la formulation VDI. Le logiciel Cobra V6 développé par le CETIM est basé sur les formules VDI 2230. Les comparaisons entre les résultats issus de notre méthode d’homogénéisation et Cobra V6 sont présentées pour un assemblage boulonné constitué de deux plaques circulaires d’aluminium 7075T6 (Tab. 5). Les simulations éléments finis ont été menées en axisymétrique à l’aide du code Cast3M. La figure 6 représente l’évolution des souplesses de la zone assemblée en fonction des diamètres des plaques Dp. La figure 7 représente pour les mêmes conditions de serrage l’évolution de la souplesse du boulon. Il convient de noter que l’approche numérique développée ne fait aucune hypothèse sur l’isotropie du matériau. En conséquence, la démarche proposée est applicable pour un assemblage de matériaux composite à comportement élastique orthotrope [9]. La souplesse calculée par éléments finis peut être identifiée à un modèle de barre ou de poutre comme préconisé dans [1–3].
Un effet de troncature du cône de Rötscher apparaît dans le sens de la largeur des éprouvettes lorsqu’on réduit les diamètres des échantillons Dp (Fig. 6).. Cette troncature est automatiquement prise en compte dans l’élaboration du modèle homogénéisé basé sur la souplesse de la zone géométrique définie par l’iso zéro en énergie définie par  .
.
Le critère énergétique peut également servir à calculer la souplesse du boulon. Les valeurs obtenues sont autour de 2,45 × 10−6 mm/N. La variation autour de cette valeur n’excède pas 1 %. Nous pouvons, afin de vérifier cette valeur, apprécier analytiquement la souplesse du boulon en appliquant la formule suivante δb = Lp/(ES) avec Lp la hauteur serrée, E le module de Young et S la section au niveau du fut. L’application numérique est effectuée pour les mêmes paramètres du boulon que ceux intégrés dans le modèle E.F. Nous avons Lp = 12 mm, E = 2,10 × 105 MPa et S = 28,27 mm2. Ce calcul nous donne une souplesse du boulon de 2,02 × 10−6 mm/N. Un écart de 17 % entre le résultat du modèle EF et celui de cette approximation analytique simplifiée est constaté (Fig. 7, Tab. 6).
La figure 8 représente l’évolution des souplesses en fonction du diamètre externe pour des pièces en matériau composite T700/PA66 d’épaisseur 6 mm et 12 mm. Les résultats sont obtenus à partir des simulations éléments finis Cast3M et du critère énergétique. Les courbes indiquent une chute brutale des valeurs des souplesses pour des diamètres externes des pièces inférieurs à 28 mm. Au-delà de cette valeur seuil, la diminution des souplesses est plus progressive. La troncature du cône de pression explique cette évolution des souplesses en fonction du diamètre du domaine Dp. La troncature de la forme de la zone de reprise des efforts est illustrée dans le tableau 6 pour les diamètres Dp. de 21 à 28 mm. Cette zone de reprise des efforts n’est pas tronquée pour les diamètres Dp de 32 à 48 mm.
Comparaison des calculs de souplesses des modèles E.F. pour l’aluminium 7075T6 et des résultats obtenus sous COBRA, logiciel de dimensionnement des assemblages boulonnés du CETIM.
Comparison between finite element flexibility models for aluminium 7075T6 and results obtained with COBRA, CETIM’s bolted joint design software.
 |
Fig. 6 Résultats analytiques et numériques des souplesses δp de pièces pour un aluminium en fonction du diamètre Dp. Analytical and numerical results of the flexibility δp of an aluminium part as a function of its diameter Dp. |
 |
Fig. 7 Évolution de la souplesse du boulon δb pour différents diamètres de pièces en aluminium Dp. Bolt flexibility evolution δb for different diameters Dp of aluminium parts. |
Calculs sur le code éléments finis Cast3M CEA – T700/PA66 Ep 12 mm – E3 = 4248 MPa.
Simulations with the finite element code Cast3M CEA – T700/PA66 Ep 12 mm – E3 = 4248 MPa.
 |
Fig. 8 Résultats des souplesses obtenus sous Cast3M pour le tissu T700/PA66 avec des épaisseurs de 6 et 12 mm. Flexibilities obtained with the code Cast3M for the fabric T700/PA66 thicknesses evolution of 6 to 12 mm. |
3.2 Démonstration des formules de souplesses de la recommandation VDI 2230 ou NF25030
La démonstration des formules de souplesse préconisée dans la VDI 2230 (2003) n’est pas publiée dans le document d’origine VDI ni dans la norme NFE 25030 ni dans la littérature. Il est donc intéressant de fournir une démonstration de ce résultat afin de mieux comprendre les limitations de cette approche [3]. Dans la suite, le raisonnement est uniquement effectué pour le cas d’un assemblage boulonné centré avec un diamètre de pièce Dp > Dpmax. Le diamètre maximum du cône de compression est noté Dpmax. La forme conique n’est donc pas tronquée dans le cas traité (Fig. 9).
Un effort F implique une variation de déplacement dU sur un élément de hauteur dz. On peut donc écrire cet effet sous la forme suivante :
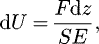 (7)
avec E le module d’Young hors plan et S la section (couronne de rayon externe r1 et de rayon interne r0). Cette section peut s’exprimer sous la forme :
(7)
avec E le module d’Young hors plan et S la section (couronne de rayon externe r1 et de rayon interne r0). Cette section peut s’exprimer sous la forme :
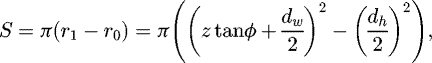 (8)et être factorisée comme suit :
(8)et être factorisée comme suit :
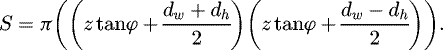 (9)
(9)
La relation (7) peut alors s’écrire en fonction de l’équation (7) et devient :
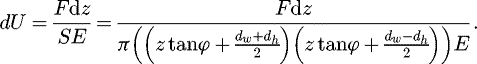 (10)
(10)
Le problème consiste alors à calculer l’intégrale suivante :
 (11)
(11)
Une technique connue pour calculer ce type d’intégrale est d’utiliser la décomposition en éléments simples. Nous nous intéressons maintenant au terme suivant :
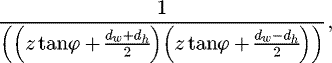 (12)
qui s’écrit de manière simplifiée comme :
(12)
qui s’écrit de manière simplifiée comme :
 (13)
(13)
Nous effectuons la résolution du système pour x = 0 et x = 1, ce qui nous donne :
 (14)
(14)
L’équation (13) s’exprime alors comme suit :
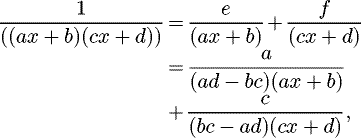 (15)
et l’intégrale à résoudre devient :
(15)
et l’intégrale à résoudre devient :
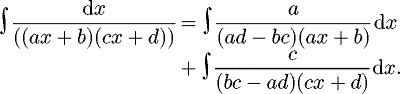 (16)
(16)
Puisque a, b, c et d sont des constantes, nous obtenons in fine l’intégrale suivante :
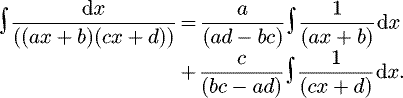 (17)
(17)
La primitive de l’équation (17) peut alors s’écrire :
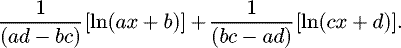 (18)
(18)
L’intégrale à résoudre devient alors :
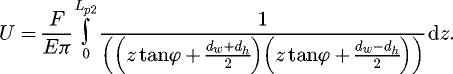 (19)
(19)
La résolution de l’équation (19) nous donne :
 (20)
(20)
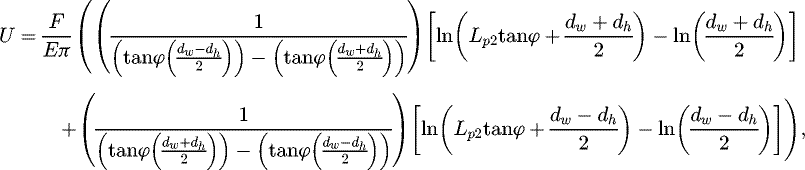 (21)
(21)




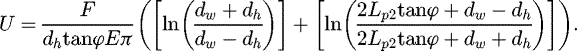
Cette démarche permet bien de retrouver la formulation en souplesse δp de la VDI 2230 (2003) reprise dans la NF25030 pour le cas d’un assemblage boulonné centré et Dp > Dpmax, le cône de reprise des efforts est non tronqué [10].
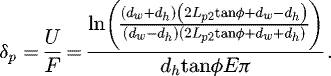 (22)
(22)
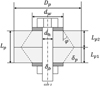 |
Fig. 9 Géométrie et notations utilisées – cas d’un chargement axial sur un assemblage centré. Geometry and notations used – case of an axial loading on a centered assembly. |
4 Conclusions et perspectives
L’étude présentée s’inscrit dans une démarche de dimensionnement hors plan d’assemblages boulonnés composites à matrice thermoplastique. Un travail expérimental de caractérisation des propriétés mécaniques du T700/PA66 est réalisé. Ensuite, une procédure homogénéisation classique est proposée pour reconstruire les propriétés élastiques tridimentionelles du Volume Élémentaire Représentatif de materiau composite. Une procedure d’homogeneisation est proposée pour évaluer les souplesses des pièces d’un assemblage boulonné. L’approche proposée est développée avec un comportement élastique, cependant elle peut être étendue à des comportements mécaniques non linéaires. Dans ce cas, la souplesse serait déterminée en fonction de l’évolution du chargement ou du temps. Le comportement mécanique des plaques composites etant issu des essais mécaniques et de la procedure d’homogeneisation réalisée sur le VER. Enfin, la démonstration des formules analytiques de souplesses proposée dans la VDI 2230 est réalisée. Ces développements analytiques et numériques sont, dans un premier temps, focalisés sur un assemblage d’aluminium 7075T6. Les résultats obtenus ont permis de valider les méthodologies proposées. Cette étude doit être complétée de manière à quantifier l’évolution de la précharge de la liaison boulonnée en fonction de la teneur en eau ou de l’évolution de la température dans le cas de stratifié T700/PA66.
Références
- NF E 25-030-1, Assemblages vise à filetage métrique partie : règle de conception des assemblages précontraints démarche simplifiée, 23 août 2014 [Google Scholar]
- NF E 25-030-2, Assemblages vise à filetage métrique partie : règle de conception des assemblages précontraints démarche complète, 23 août 2014 [Google Scholar]
- VDI 2230 BLATT 1, Systematische Berechnung Hochbeanspruchter Schraubenver-bindungen Zylindrische Einschraubenverbindungen, VDI Richtlinien, ICS 21.060.10, VDI-Gesellschaft Entwicklung Konstruktion Vertrieb, Fachberuch Konstruktion, Ausschuss Schraubenverbindungen, pp. 1–169, 2003 [Google Scholar]
- Rotscher. Die Maschinenelemente, Springer-Verlag, Berlin, Germany, 1927 [Google Scholar]
- A. Krasnobrizha, P. Rozycki, L. Gornet, P. Cosson, Hysteresis behaviour modelling of woven composite using a collaborative elastoplastic damage model with fractional derivative, Compos. Struct. 158, 101 (2016) [CrossRef] [Google Scholar]
- K.N. Shivakumar, H.J. Crews, JR, Bolt clampup relaxation in a Graphite/epoxy laminate, NASA Technical Memorandum, 1982, vol. 83268, 32 p. [Google Scholar]
- V. Caccese, K.A. Berube, M. Fernandez, J. Daniel Melo, J.P. Kabche, Influence of stress relaxation on clamp-up force in hybrid composite-to-metal bolted joints, Compos. Struct. 89(2), 285 (2009) [CrossRef] [Google Scholar]
- A. Daidie, J. Chakhari, A. Zghal, Numerical model for bolted T-stubs with two bolt rows, Struct. Eng. Mech. 26(3), 343 (2007) [CrossRef] [Google Scholar]
- L. Gornet, G. Marckmann, M. Lombard, Des coefficients d’élasticité et de rupture d’âmes nids d’abeilles Nomex : homogénéisation périodique et simulation numérique, Méc. Ind., Elsevier 1(3), 267 (2000) [Google Scholar]
- R. Hamonou, Contribution à l’analyse du comportement hors plan des assemblages boulonnés, Thèse GeM, École Centrale de Nantes – Université de Nantes, 2016 [Google Scholar]
Citation de l’article : Laurent Gornet, Romain Hamonou, Frédéric Jacquemin, Stéphane Auger, Pierre Chalandon, Détermination de la souplesse hors plan d’un assemblage de composites boulonnés à l’aide d’une démarche d’homogénéisation, Matériaux & Techniques 106, 302 (2018)
Liste des tableaux
Propriétés élastiques du tissu équilibré T700/PA66.
Elastic properties of the balanced fabric T700/PA66.
Valeurs expérimentales du module hors plan du T700/PA66 en fonction de son épaisseur.
Experimental values of the out-of-plane module of the T700/PA66 as a function of its thickness.
Propriétés élastiques du toron de fibres T700/PA66 utilisé dans les simulations EF.
Elastic properties of the fibers’ strand T700/PA66 used in finite element simulations.
Propriétés élastiques homogénéisées du tissu T700/PA66.
Homogenized elastic properties of the T700/PA66 fabric.
Comparaison des calculs de souplesses des modèles E.F. pour l’aluminium 7075T6 et des résultats obtenus sous COBRA, logiciel de dimensionnement des assemblages boulonnés du CETIM.
Comparison between finite element flexibility models for aluminium 7075T6 and results obtained with COBRA, CETIM’s bolted joint design software.
Calculs sur le code éléments finis Cast3M CEA – T700/PA66 Ep 12 mm – E3 = 4248 MPa.
Simulations with the finite element code Cast3M CEA – T700/PA66 Ep 12 mm – E3 = 4248 MPa.
Liste des figures
 |
Fig. 1 Assemblage de deux pièces mécaniques par une liaison boulonnée. L’effort exercé par le boulon est repris dans les deux pièces par des zones tronc coniques creuses à 45° (cônes de Rötscher). Assembly of two mechanical parts by a bolted connection. The force exerted by the bolt is taken up in both parts by 45° hollow conical trunks (Rötscher cones). |
| Dans le texte | |
 |
Fig. 2 Dimensions nominales des éprouvettes en mm. Nominal specimen dimensions in mm. |
| Dans le texte | |
 |
Fig. 3 Comportement dans le sens chaîne [0°]. Behaviour in the chain direction [0°]. |
| Dans le texte | |
 |
Fig. 4 Comportement en cisaillement plan [± 45°]. Évolution des modules sécants. Plane shear behaviour [± 45°]. Evolution of secant modules. |
| Dans le texte | |
 |
Fig. 5 Volume Élémentaire Représentatif du Tissu T700/Pa66 voxélisé utilisé pour l’homogénéisation. Representative Elementary Volume of the T700/Pa66 voxelized fabric used for homogenization. |
| Dans le texte | |
 |
Fig. 6 Résultats analytiques et numériques des souplesses δp de pièces pour un aluminium en fonction du diamètre Dp. Analytical and numerical results of the flexibility δp of an aluminium part as a function of its diameter Dp. |
| Dans le texte | |
 |
Fig. 7 Évolution de la souplesse du boulon δb pour différents diamètres de pièces en aluminium Dp. Bolt flexibility evolution δb for different diameters Dp of aluminium parts. |
| Dans le texte | |
 |
Fig. 8 Résultats des souplesses obtenus sous Cast3M pour le tissu T700/PA66 avec des épaisseurs de 6 et 12 mm. Flexibilities obtained with the code Cast3M for the fabric T700/PA66 thicknesses evolution of 6 to 12 mm. |
| Dans le texte | |
 |
Fig. 9 Géométrie et notations utilisées – cas d’un chargement axial sur un assemblage centré. Geometry and notations used – case of an axial loading on a centered assembly. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




