| Issue |
Matériaux & Techniques
Volume 106, Number 2, 2018
|
|
|---|---|---|
| Article Number | 203 | |
| Number of page(s) | 13 | |
| Section | Comportement en service / Behaviour in service | |
| DOI | https://doi.org/10.1051/mattech/2018038 | |
| Published online | 17 October 2018 | |
Regular Article
Influence du type de démarche de fatigue multiaxiale sur la prévision de durée de vie d’un assemblage boulonné
Influence of multiaxial fatigue gait type on bolted joint life assessment
1
Université Clermont Auvergne, CNRS, Institut Pascal,
63000
Clermont-Ferrand, France
2
SNCF RESEAU, Direction Ingénierie & projets, Département Lignes Voie Environnement (LVE),
Saint Denis, France
* e-mail: aliou_badara.camara@etudiant.univ-bpclermont.fr
Reçu :
23
Octobre
2017
Accepté :
5
Juillet
2018
Ce travail présente l’étude de l’évaluation de la durée de vie en fatigue d’un joint éclissé de rail en utilisant deux critères de fatigue multiaxiaux. Le premier critère, basé sur l’approche de type plan critique, est celui de Dang Van. C’est un critère largement utilisé pour les applications industrielles en France. Pour certaines conditions de chargement, en particulier lorsque la structure est soumise à des états de contraintes non proportionnels, l’approche plan critique ne fournit pas toujours une durée de vie conservative en fatigue. C’est la raison pour laquelle un autre critère, basé sur une approche différente de fatigue multiaxiale, a été implémenté et mis en œuvre. Le second critère relève de l’approche intégrale proposée par Zenner. Ces deux critères sont programmés sur le logiciel Matlab pour le calcul de la durée de vie en fatigue multiaxiale. Des différences significatives sont obtenues selon l’approche de fatigue multiaxiale utilisée.
Abstract
This work presents the study of the fatigue life assessment of bolted rail joint using two multiaxial fatigue criteria. The first one is based on the critical plane approach. It uses Dang Van’s criterion, that is widely employed for industrial applications in France. For some loading conditions, especially when the structure is submitted to non-proportional loads, the critical plane approach do not always provide conservative fatigue life. It is the reason why a second multiaxial fatigue criterion approach has been developed and implemented based on the integral concept (Zenner’s criterion). These two criteria are implemented on Matlab software for fatigue life calculation purpose. Significant differences are obtained according to the multiaxial fatigue approach.
Mots clés : fatigue / durée de vie / critère multiaxial / assemblage éclissé
Key words: fatigue / lifetime / multiaxial criterion / bolted rail joint
© A.B. Camara et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Les assemblages boulonnés sont sans nul doute l’un des systèmes de liaison les plus utilisés dans l’industrie mécanique pour réaliser une liaison complète démontable entre deux composants. Ils font parfois l’objet de méthodes de dimensionnement rudimentaires, qui conduisent dans la plupart des cas à les surdimensionner de manière considérable sans pour autant en garantir la sécurité [1]. L’assemblage boulonné est un élément de structure au comportement complexe qui n’a sans doute pas encore fait l’objet de tous les travaux de recherche que son importance dans la construction mécanique justifierait. Ce type d’assemblage est souvent utilisé dans le domaine ferroviaire notamment (assemblage éclissé). L’augmentation sans cesse croissante de la charge de l’essieu, de la vitesse des trains (TGV) et du volume du trafic a entraîné des coûts d’entretien importants engendrés par l’usure et la fatigue des matériaux. Chaque année des frais de maintenance considérables sont ainsi consacrés à l’infrastructure ferroviaire en Europe. Parallèlement de nombreux chercheurs [2–4] se sont intéressés à l’étude en fatigue de l’assemblage éclissé pour analyser l’influence de certains paramètres :
-
influence des types de joints (joints supportés et joints suspendus) ;
-
influence de la dégradation du support de ballast sur l’assemblage qui engendre une flèche importante au passage des roues ;
-
influence du nombre de boulons de l’assemblage (éclisses à 4 boulons et éclisses à 6 boulons).
Cet article propose une méthodologie de calcul de la durée de vie d’un assemblage boulonné (pour le dimensionnement de l’ensemble des composants qui le composent) en se basant dans un premier temps sur le critère d’approche plan critique de Dang Van. Lorsque la structure est soumise à des chargements non proportionnels (déphasage des composantes du tenseur des contraintes), l’approche plan critique en fatigue multiaxiale ne permet pas toujours une prévision de durée de vie réaliste. Aussi un deuxième critère multiaxial de type approche intégrale (critère de Zenner) est utilisé pour analyser le chargement multiaxial.
2 Présentation de l’assemblage éclissé
Lorsqu’on construit et maintient un réseau ferroviaire, un des points d’attention les plus importants concerne les assemblages éclissés. On nomme éclisses deux armatures en acier laminé destinées à relier au moyen de boulons les extrémités des rails et assurer ainsi la continuité de la voie. Les éclisses assemblent deux abouts de rails en prenant appui sous le champignon du rail et sur la partie inclinée de son patin ; elles sont assemblées par 4 ou 6 boulons. L’assemblage complet de deux rails et de deux éclisses s’appelle un joint. Lorsque les deux éclisses sont serrées de part et d’autre des rails par leurs boulons, on peut considérer qu’il y a encastrement. Si une charge agit à l’extrémité d’un rail A, celui-ci transmet aux éclisses cette charge et il faut que l’autre éclisse, encastrée dans le rail B la supporte sans fléchir (Fig. 1). Les éclisses permettent non seulement d’assurer un bon contact électrique entre les éléments de voie mais aussi de respecter la géométrie de l’ensemble et donc d’assurer un bon roulement. Les éclisses sont souvent utilisées à proximité des aiguillages ou autres appareils de voie. En pleine voie, la jonction entre deux rails se fait généralement par soudure. Dans le but d’étudier l’assemblage éclissé, une modélisation par éléments finis a été faite sur ANSYS.
 |
Fig. 1 Description de l’assemblage éclissé de 2 rails. Description of one jointed rail assembly. |
3 Modélisation par éléments finis de l’assemblage
La modélisation par éléments finis de l’assemblage éclissé s’appuie sur plusieurs hypothèses importantes :
-
les contraintes résiduelles dues à la fabrication ne sont pas considérées et les effets de la température ne sont pas étudiés ;
-
la présence de défauts de surface (rayures,…) n’est pas prise en compte, tout comme un mauvais positionnement des éclisses ;
-
le calcul est statique. L’aspect dynamique est pris en compte en appliquant un coefficient multiplicateur c sur les efforts au niveau de la lacune (entrefer). Ce coefficient a été calculé précédemment lors d’une simulation du comportement dynamique par une société externe (VibraTec) et est égal à 2 ;
-
le frottement rail/éclisses et éclisses/boulons est considéré statique dans cette modélisation ;
-
le filetage du boulon n’est pas modélisé.
3.1 Géométrie
L’assemblage éclissé est modélisé de sorte à pouvoir tester tout type de joint éclissé ordinaire, à 4 ou à 6 boulons, pour des rails 50 kg ou 60 kg, pour plusieurs profils d’éclisses, pour différentes longueurs d’éclisses et un entrefer variable, etc. En vue de la réalisation ultérieure du maillage sous ANSYS, les géométries sont découpées et simplifiées (par la suppression de certains arrondis notamment). L’étude présentée dans cet article concerne un joint éclissé ordinaire U50 comportant 4 boulons (Fig. 2).
Profil Rail U50 selon VV16122_000018 C
Eclisse 4T U95 selon VV16131_000053 F
La géométrie des boulons nécessite également une simplification, d’une part parce que le maillage du filetage serait très difficile à réaliser, d’autre part parce que le procédé de fabrication (roulage) implique la présence de contraintes résiduelles importantes qui ne sont pas parfaitement connues. Le comportement des filets ne sera donc pas étudié ici. On conserve simplement dans le modèle le diamètre du fût et le diamètre équivalent de traction (17,65 mm pour les boulons M20-125, Fig. 3).
 |
Fig. 2 Géométrie simplifiée et découpée − Creo Parametric. Simplified and cut geometry according to Creo Parametric. |
 |
Fig. 3 Géométrie simplifiée des boulons − Creo Parametric. Simplified geometry of bolts according to Creo Parametric. |
3.2 Matériau
La construction du modèle sous forme de briques assemblées offre la possibilité d’affecter des matériaux différents pour chaque composant : rail droite, rail gauche, vis, écrous, éclisses, etc. Dans l’étude et le calcul des contraintes qui suit, le matériau utilisé est le même pour tous les composants du point de vue des propriétés mécaniques statiques du domaine élastique. Le module de Young E est égal à 210 GPa et le coefficient de Poisson est de 0,3. Le comportement adopté pour les calculs est élastique isotrope. Les traverses sont modélisées comme étant rigides. Les contacts entre les différents composants de l’assemblage prennent en compte le frottement (Fig. 4). Le modèle de frottement implémenté sous ANSYS est une approximation de la loi de Coulomb. On a glissement entre les surfaces en contact lorsque la contrainte de frottement excède une valeur τmax (Fig. 4) calculée à partir de la valeur du coefficient de frottement rentré par l’utilisateur. L’approximation de la loi de Coulomb consiste en une transition lissée entre l’état collé (sticking) et l’état de glissement (sliding) par une droite de pente m (cette pente étant théoriquement infinie dans la loi de Coulomb).
Ce modèle correspond à un frottement statique, le coefficient reste constant lors du glissement. Il ne tient pas compte du frottement dynamique qui implique que la valeur du coefficient change (diminue) lors de la phase de glissement.
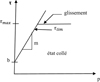 |
Fig. 4 Modèle de frottement proposé par ANSYS. Friction model proposed by ANSYS code. |
3.3 Maillage
La réalisation d’un maillage régulier au niveau des contacts rails-éclisses est indispensable, sauf à connaître des problèmes de temps de calcul, de précision et de convergence. L’intérêt des découpes est de pouvoir piloter sur chaque segment le nombre d’éléments (et leur taille) de manière à obtenir un maillage régulier et paramétré où les nœuds des surfaces en contact sont en vis-à-vis. Le modèle comporte 157045 éléments linéaires (192842 nœuds). La figure 5 donne un aperçu du maillage de l’assemblage global.
ANSYS Workbench dispose d’un module de serrage des boulons, simple d’utilisation. En effet, le module coupe automatiquement le boulon en deux parties et insère les éléments de pré-tension (Fig. 6). Le nœud de pré-tension K est destiné à controler les charges de tension totales. Le serrage du boulon est alors verrouillé, permettant l’application d’autres efforts en superposition.
La force de serrage initiale a été fixée à 50 kN par boulon, ce qui correspond à l’effort généré par un couple de 200 Nm environ sur un boulon standard graissé.
 |
Fig. 5 Maillage d’un joint éclissé et zones de contact − ANSYS Workbench. Splined joint meshing and contact zones according to ANSYS Workbench. |
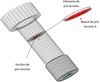 |
Fig. 6 Modèle permettant le serrage des boulons (logiciel ANSYS). Model for tightening bolts (ANSYS code). |
3.4 Conditions aux limites
Le modèle de joint éclissé mesure 4800 mm (il est suffisamment long pour qu’il n’y ait pas d’effet de bord au niveau de la zone étudiée). Les deux extrémités du rail sont bloquées dans la direction longitudinale Z (Fig. 7). De même, les faces latérales des traverses (de couleur jaune) sont bloquées en déplacement suivant X et Z (suppression des modes de corps rigides).
 |
Fig. 7 Définition des conditions aux limites : utilisation des symétries. Boundary conditions and use of symmetries. |
4 Discrétisation du chargement rencontré lors du passage d’une roue sur l’assemblage
Le passage d’une roue du train sur le rail est modélisé par une succession d’efforts appliqués (sept au total) l’un après l’autre et un à la fois (Fig. 8). Une seule roue est considérée ici. Le chargement statique (effort vertical à la roue) est de 112,5 kN. La surcharge dynamique est modélisée par un coefficient multiplicateur c appliqué à l’effort statique. Ce coefficient est calculé via un modèle numérique développé par VibraTec et vaut 2 dans cette étude.
Les résultats qui sont présentés par la suite en termes de contraintes sont obtenus avec ces sept chargements consécutifs décrivant le passage de la roue sur l’assemblage. En un nœud du boulon et un nœud du rail, les différentes composantes de la matrice des contraintes, exprimées en MPa, varient au cours du passage de la roue telles que décrites par la figure 9.
Les états de contraintes rencontrés localement sont le plus souvent multiaxiaux. Cette triaxialité des états de contrainte doit être prise en compte dans l’analyse du comportement en fatigue de l’assemblage et du boulon en particulier. Ainsi les critères de fatigue multiaxiaux sont les outils adaptés pour l’évaluation de la résistance en fatigue du matériau soumis à un état de contrainte périodique.
 |
Fig. 8 Application des chargements successifs traduisant le passage d’une roue sur l’assemblage éclissé. Successive loads events corresponding to one wheel rolling over the splined assembly. |
 |
Fig. 9 Évolution du tenseur des contraintes (en MPa) au cours du passage d’une roue sur l’assemblage (cycle). Stress states cycle (in MPa) corresponding to one wheel rolling over the splined assembly. |
5 Fatigue multiaxiale
Toute pièce mécanique est soumise durant son fonctionnement en service à des sollicitations d’origines variables et qui se traduisent localement par des états de contraintes cycliques ou à amplitude variable. Dans ces conditions il est souvent constaté la ruine progressive (endommagement) en service des structures alors que celles-ci ne sont soumises qu’à des sollicitations jugées modestes par rapport aux capacités statiques des matériaux. L’origine de ces ruines est le plus souvent le phénomène de fatigue [5]. Selon que la sollicitation rencontrée engendre un état de contraintes uniaxial ou multiaxial, le dimensionnement est fait au moyen d’outils relevant soit de la fatigue uniaxiale soit de la fatigue multiaxiale. Dans notre cas, les critères de fatigue multiaxiaux sont utilisés car les états de contraintes analysés sont multiaxiaux. L’utilisation des critères de fatigue requiert la connaissance du comportement en fatigue du matériau utilisé, représenté généralement à l’aide de plusieurs courbes S−N. Ces courbes traduisent la relation entre la contrainte appliquée et le nombre de cycles à rupture, mettant au passage en évidence la notion de limite de fatigue qui correspond à la contrainte en dessous de laquelle il n’y a pas de risque de rupture par fatigue quel que soit le nombre de cycles appliqués (Fig. 10).
Deux critères de fatigue multiaxiaux sont utilisés dans cette étude :
-
le critère de Dang Van (critère d’approche plan critique) ;
-
le critère de Zenner (critère d’approche intégrale).
 |
Fig. 10 Allure générale d’une courbe S-N d’un matériau métallique (d’après [6]). General feature of metal S-N curves. |
5.1 Le critère de Dang Van
Le critère de Dang Van, dans sa première version (1973), est le premier critère de fatigue à avoir été introduit dans l’industrie française (chez PSA). Justifié à l’origine par des considérations établies à l’échelle microscopique, le critère utilise des grandeurs macroscopiques des contraintes qui sont la partie alternée du cisaillement τha et la pression hydrostatique p [7–9]. La fonction de fatigue EDV du critère est une maximisation de l’indicateur de dommage par plan Eh, défini sur le plan de normale h par :
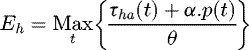 (1)
(1)
Où 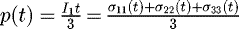 ,
I1(t) est le premier invariant du tenseur des contraintes,
,
I1(t) est le premier invariant du tenseur des contraintes,
τha(t) est la contrainte tangentielle alternée qui agit sur le plan de normale h à l’instant t et est déterminée à l’aide du plus petit cercle circonscrit au trajet de chargement [7,10].
Le plan où Eh est maximal est appelé plan critique. C’est lui qui permet au critère de traduire la sévérité du chargement multiaxial rencontré.
La fonction de fatigue du critère s’écrit alors :
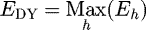 (2)
Par définition, la fonction de fatigue du critère est égale à l’unité lorsque la limite de fatigue du matériau est atteinte, en particulier pour les limites de fatigue en traction alternée symétrique (σ-1) et en torsion alternée symétrique (τ-1) qui servent au calage du critère. Les paramètres α et θ sont données par :
(2)
Par définition, la fonction de fatigue du critère est égale à l’unité lorsque la limite de fatigue du matériau est atteinte, en particulier pour les limites de fatigue en traction alternée symétrique (σ-1) et en torsion alternée symétrique (τ-1) qui servent au calage du critère. Les paramètres α et θ sont données par :
 La condition de validité du critère de Dang Van s’écrit
La condition de validité du critère de Dang Van s’écrit 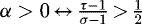
5.2 Le critère de Zenner
Ce critère définit son indicateur d’endommagement par plan par l’expression [11] :
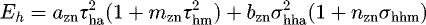 (3)
La fonction de fatigue du critère est établie par une moyenne de l’indicateur par plan Eh sur tous les plans matériels possibles :
(3)
La fonction de fatigue du critère est établie par une moyenne de l’indicateur par plan Eh sur tous les plans matériels possibles :
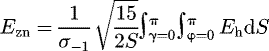 (4)Où S = 2π (aire de la surface d’une demi-sphère de rayon unité) et
(4)Où S = 2π (aire de la surface d’une demi-sphère de rayon unité) et 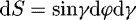
Le critère proposé par Zenner comporte quatre constantes notées ici azn, bzn, mzn et nzn qui sont établies à partir de quatre limites de fatigue en traction alternée symétrique σ-1, en torsion alternée symétrique τ-1, en traction répétée σ0 et en torsion répétée τ0. L’une d’entre elles (en torsion répétée τ0) peut être estimée à partir des 3 autres limites de fatigue σ-1, τ-1 et σ0, à l’aide de la relation empirique suivante [11,12] :
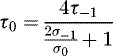 (5)
Le critère fait intervenir deux termes relatifs aux contrainte tangentielles (τha et τhm) et deux autres relatifs aux contraintes normales (σhha et σhhm) agissant sur le plan de normale unitaire h :
(5)
Le critère fait intervenir deux termes relatifs aux contrainte tangentielles (τha et τhm) et deux autres relatifs aux contraintes normales (σhha et σhhm) agissant sur le plan de normale unitaire h :
τha et τhm: amplitude et valeur moyenne de la contrainte tangentielle sur le plan de normale h,
σhha et σhhm amplitude et valeur moyenne de la contrainte normale au plan de normale h.
Les constantes obtenues par le calage du critère sur les 4 limites de fatigue sont :
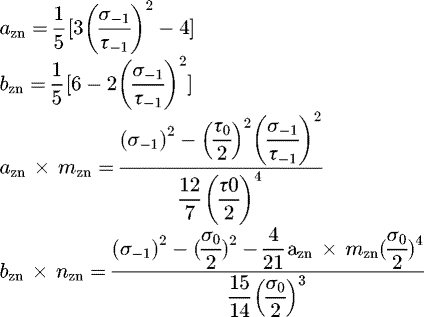
6 Endommagement et durée de vie en fatigue
6.1 Prévision de durée de vie en fatigue
Le cahier des charges qui concerne le dimensionnement en fatigue des structures peut se résumer de la façon suivante : il n’est pas seulement besoin de savoir aujourd’hui si une avarie de fatigue surviendra un jour ou ne se produira jamais, mais de déterminer quand elle apparaîtra. De ce fait, on ne se contente plus de vérifier si une structure ou un composant mécanique travaille ou non au seuil de son endurance illimitée. On établit sa durée de vie, c’est-à-dire le nombre N de cycles qui peuvent être appliqués à l’amorçage d’une fissure (ou à la rupture du composant). Ce calcul de la durée de vie en fatigue est mené en utilisant une démarche itérative employant les critères de fatigue multiaxiaux étendus au domaine de l’endurance limitée.
Pour calculer la durée de vie en fatigue de manière itérative, l’endommagement (la fonction de fatigue du critère multiaxial) est calculé tout d’abord au seuil de l’endurance illimitée. Cet endommagement est noté E1 et la durée de vie au seuil de l’endurance illimitée est notée N1. Ensuite l’endommagement est calculé à l’autre extrémité du domaine de l’endurance limitée de la courbe S-N et est noté E2 avec comme durée de vie N2 (N2 < N1). La démarche itérative consiste entre autres à discuter de la valeur de ces endommagements, pour en tirer certains renseignements.
-
si E1 < 1, alors la durée de vie sera considérée comme infinie ;
-
si E2 > 1, alors la durée de vie est inférieure à la dernière valeur de N2 mais dans ce cas le problème est celui d’un calcul de durée de vie dans le domaine oligocyclique ;
-
si E1>1 et E2 < 1, dans ce cas une méthode de dichotomie est utilisée pour réduire l’intervalle jusqu’à converger vers la valeur de la durée de vie N définie par :
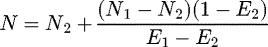 La condition de convergence est que la fonction de fatigue E(N) soit égale à l’unité lorsque la durée de vie du matériau est atteinte. La figure 11 donne l’algorithme de la démarche itérative du calcul de durée de vie en fatigue proposée et implémentée sous le logiciel MATLAB.
La condition de convergence est que la fonction de fatigue E(N) soit égale à l’unité lorsque la durée de vie du matériau est atteinte. La figure 11 donne l’algorithme de la démarche itérative du calcul de durée de vie en fatigue proposée et implémentée sous le logiciel MATLAB.
Les courbes S-N réelles des matériaux utilisés pour les rails et pour les boulons ne sont pas connues précisément dans le cadre de cette étude. Le calcul de l’endommagement et celui de la durée de vie en fatigue sont donc réalisés en utilisant des matériaux similaires, dont les courbes S-N (modèle de Wöhler) en traction alternée symétrique (σ-1 (N), en MPa) sont les suivantes :
Courbe S-N du rail : σ-1 (N) = 547 – 31.log(N)
Courbe S-N du boulon : σ-1 (N) = 232 – 31.log(N)
Les courbes de fatigue sous sollicitation de torsion sont plus difficiles à obtenir en pratique. Elles sont ici établies à partir de celles en traction alternée symétrique. Pour cela un rapport égal à 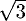 est utilisé (soit
est utilisé (soit 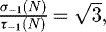 [12]). L’algorithme de l’outil de post-traitement développé sous Matlab pour le critère de Dang Van est donné à la figure 13. Celui élaboré pour le critère de Zenner est similaire dans son principe ; tous les plans matériels possibles doivent avoir été traités (Fig. 12) pour le critère de Dang Van afin de déterminer le plan critique, et pour le critère d’approche intégrale pour obtenir la moyenne référente de l’indicateur d’endommagement Eh.
[12]). L’algorithme de l’outil de post-traitement développé sous Matlab pour le critère de Dang Van est donné à la figure 13. Celui élaboré pour le critère de Zenner est similaire dans son principe ; tous les plans matériels possibles doivent avoir été traités (Fig. 12) pour le critère de Dang Van afin de déterminer le plan critique, et pour le critère d’approche intégrale pour obtenir la moyenne référente de l’indicateur d’endommagement Eh.
 |
Fig. 11 Démarche itérative de calcul de durée de vie en fatigue multiaxiale avec les critères de Dang Van ou de Zenner. Life assessment procedure under multiaxial constant amplitude fatigue by the use of Dang Van or Zenner criterion. |
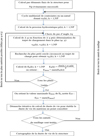 |
Fig. 13 Organigramme du calcul de durée de vie en fatigue multiaxiale avec le critère de Dang Van. Multiaxial fatigue life assessment according to Dang Van criterion. |
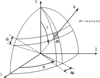 |
Fig. 12 Concept mathématique de Simbüger pour examiner tous les plans matériels passant par un point matériel (ou nœud). Parametric definition of one material plane according to Simbürger denotations. |
6.2 Influence du type de démarche (approche plan critique vs approche intégrale)
Les calculs de la fonction de fatigue (endommagement) au seuil de l’endurance illimitée, selon chacun des deux critères utilisés, ont été conduits pour l’ensemble de l’assemblage éclissé. Les deux critères conduisent aux mêmes zones critiques sur le rail (Fig. 14) et sur le boulon (Fig. 15). Les zones critiques (zones d’amorçage de fissures) sont, pour le rail, le congé âme-champignon (Fig. 14a), le premier trou après la lacune (Fig. 14b) et le congé âme-patin (Fig. 14c), et la jonction tête-fût pour le boulon (Fig. 15b).
Bien que les deux critères de fatigue aient conduit aux mêmes zones critiques sur le rail et sur le boulon, les valeurs des fonctions de fatigue sont très différentes. Au niveau du nœud 26569, nœud le plus sollicité du congé âme − champignon, la fonction de fatigue selon le critère de Dang Van vaut 0,085 alors qu’elle vaut 0,0498 pour le critère de Zenner. De même, pour le nœud le plus sollicité de la jonction tête-fût de la vis (nœud 28708), la fonction de fatigue est égale à 2,225 pour le critère de Dang Van et 1,25 pour celui de Zenner (Tab. 1).
La prévision de la durée de vie a ensuite été réalisée par la démarche itérative, mentionnée précédemment. La figure 9 représente à titre d’exemple le cycle multiaxial de contrainte rencontré en un nœud du rail situé à la jonction entre l’âme et le champignon et en un nœud situé à la jonction entre la tête et le fût de la vis. Le tableau 1 récapitule les résultats de calcul obtenus en ces deux nœuds.
La différence, entre les deux approches étudiées, de la perception de la sévérité en fatigue des cycles multiaxiaux rencontrés aux deux nœuds 26569 et 28708 est très sensible comme l’indique le tableau 1. La différence d’analyse entre l’approche plan critique et l’approche intégrale est manifeste pour des propriétés mécaniques en fatigue pourtant identiques, même si les propriétés des matériaux utilisés pour cette simulation numérique sont issues d’une estimation des propriétés réelles.
La figure 15 montre la cartographie de la durée de vie en fatigue du rail et de celle de la vis. Pour le chargement et les courbes S-N considérés, le calcul de la durée de vie en fatigue donne des durées de vie infinies pour le rail (Fig. 15a). Au niveau de la vis par contre les durées de vie appartiennent au domaine de l’endurance limitée (Fig. 15b). Les zones où les durées de vie en fatigue sont les plus faibles sur la vis sont d’une part la jonction entre la tête et le fût de la vis et d’autre part le premier filet de la vis en prise. En effet, ces deux zones sont le siège de concentrations de contrainte car elles correspondent à des zones de changement brusque de section. Cette analyse justifie la nécessité de la maintenance régulière effectuée sur l’assemblage éclissé.
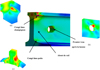 |
Fig. 14 Les zones critiques du rail en fatigue. Critical zones of the rail from the fatigue point of view. |
 |
Fig. 15 Cartographie de la durée de vie en fatigue (a) du rail, (b) de la vis. Fatigue life distribution (a) of the rail, (b) of the screw close to the assembly gap. |
Endommagement et durée de vie en deux nœuds de l’assemblage.
Fatigue damage and fatigue lifetime for two nodes of the splined assembly.
7 Conclusion
Le dimensionnement en fatigue des structures soumises à des sollicitations de fatigue est un point essentiel pour assurer leur pérennité dans l’industrie du transport, notamment dans l’automobile, dans l’aéronautique et dans le domaine ferroviaire. Les pièces de liaisons comme celles des assemblages boulonnés sont particulièrement vulnérables de ce point de vue car elles subissent à la fois les sollicitations de service transmises entre les composants ou les sous-ensembles des structures et en même temps les contraintes propres à l’assemblage, nécessaires pour réaliser pratiquement la liaison (serrage des boulons par exemple) et qui se superposent à celles rencontrées en service. Les états de contraintes rencontrés sont le plus souvent multiaxiaux.
Dans cet article, une méthodologie de calcul de durée de vie en fatigue de l’assemblage boulonné éclissé a été présentée et implémentée sous Matlab, cette méthodologie est basée sur l’utilisation des critères de fatigue multiaxiaux (Dang Van et Zenner, deux critères de natures différentes pour mesurer l’influence relative de l’approche plan critique par rapport à celle de l’approche intégrale). À propriétés des matériaux identiques, les deux approches conduisent à des résultats de prévision de comportement en fatigue différents.
Les travaux futurs visent dans un premier temps une caractérisation plus précise du comportement en fatigue des matériaux intervenant dans les assemblages (courbes S-N effectives allant jusqu’à 107 cycles), afin d’étayer de manière plus juste la comparaison des résultats obtenus avec les deux approches utilisées et présentées ici, puis la validation des outils développés au travers d’études expérimentales du comportement des assemblages boulonnés.
De cet outil d’analyse du comportement en fatigue des assemblages boulonnés pourront naître des modifications de conception mécanique, en particulier au niveau de la géométrie de ces assemblages. L’outil numérique mis en place permettra alors la simulation du comportement en fatigue de l’assemblage boulonné et ainsi l’optimisation de sa conception au regard des durées de vie escomptées.
Références
- J. Guillot, Assemblages par éléments filetés, Technique de l’Ingénieur, 62, (1989) [Google Scholar]
- D.Y. Jeong, Engineering studies on joint bar integrity, Part I: field surveys and observed failure modes, 2014, pp. 1–11 [Google Scholar]
- S. Mohammadzadeh, M. Sharavi, H. Keshavarzian, Reliability analysis of fatigue crack initiation of railhead in bolted rail joint, Eng. Fail. Anal. 29, 132 (2013) [CrossRef] [Google Scholar]
- S. Patel, V. Kumar, R. Nareliya, Fatigue analysis of rail joint using finite element method, IJRET, 2013, pp. 80–84 [Google Scholar]
- H. Rognon, Comportement en fatigue sous environnement vibratoire : prise en compte de la plasticité au sein des méthodes spectrales, École Centrale Paris (ED287), Thèse, 2013, 196 p [Google Scholar]
- E. Charkaluk, Fatigue des matériaux métalliques : quelques contributions à une approche dissipative, mémoire HDR, 2006, 79 p [Google Scholar]
- K. Dang Van, A. Le Douaron, H. P. Lieurade, Multiaxial fatigue limit: a new approach, École Polytechnique, 1984 [Google Scholar]
- K. Dang Van, B. Griveau, O. Message, On a new multiaxial fatigue limit criterion: theory and application, École Polytechnique, 1989 [Google Scholar]
- B. Weber, Fatigue multiaxiale des structures industrielles sous chargement quelconque, INSA de Lyon, Thèse, 1999, 243 p [Google Scholar]
- B. Weber, B. Kenmeugne, J.C. Clement, J.L. Robert, Improvements of multiaxial fatigue criteria computation for a strong reduction of calculation duration, Comput. Mater. Sci. 15, 381 (1999) [CrossRef] [Google Scholar]
- J. Liu, H. Zenner, Berechnung der Dauerschwingfestigkeit bei mehrachsiger Beanspruchung − Teil 1, 1993 [Google Scholar]
- T. Van Xuan, Critères multiaxiaux d’amorçage en fatigue, Code_Aster, 2013, pp. 1–45 [Google Scholar]
Citation de l’article : Aliou Badara Camara, Fabienne Pennec, Emmanuel Laurans, Vincent Peyronnet, Jean-Louis Robert, Abdelhamid Bouchaïr, Influence du type de démarche de fatigue multiaxiale sur la prévision de durée de vie d’un assemblage boulonné, Matériaux & Techniques 106, 203 (2018)
Liste des tableaux
Endommagement et durée de vie en deux nœuds de l’assemblage.
Fatigue damage and fatigue lifetime for two nodes of the splined assembly.
Liste des figures
 |
Fig. 1 Description de l’assemblage éclissé de 2 rails. Description of one jointed rail assembly. |
| Dans le texte | |
 |
Fig. 2 Géométrie simplifiée et découpée − Creo Parametric. Simplified and cut geometry according to Creo Parametric. |
| Dans le texte | |
 |
Fig. 3 Géométrie simplifiée des boulons − Creo Parametric. Simplified geometry of bolts according to Creo Parametric. |
| Dans le texte | |
 |
Fig. 4 Modèle de frottement proposé par ANSYS. Friction model proposed by ANSYS code. |
| Dans le texte | |
 |
Fig. 5 Maillage d’un joint éclissé et zones de contact − ANSYS Workbench. Splined joint meshing and contact zones according to ANSYS Workbench. |
| Dans le texte | |
 |
Fig. 6 Modèle permettant le serrage des boulons (logiciel ANSYS). Model for tightening bolts (ANSYS code). |
| Dans le texte | |
 |
Fig. 7 Définition des conditions aux limites : utilisation des symétries. Boundary conditions and use of symmetries. |
| Dans le texte | |
 |
Fig. 8 Application des chargements successifs traduisant le passage d’une roue sur l’assemblage éclissé. Successive loads events corresponding to one wheel rolling over the splined assembly. |
| Dans le texte | |
 |
Fig. 9 Évolution du tenseur des contraintes (en MPa) au cours du passage d’une roue sur l’assemblage (cycle). Stress states cycle (in MPa) corresponding to one wheel rolling over the splined assembly. |
| Dans le texte | |
 |
Fig. 10 Allure générale d’une courbe S-N d’un matériau métallique (d’après [6]). General feature of metal S-N curves. |
| Dans le texte | |
 |
Fig. 11 Démarche itérative de calcul de durée de vie en fatigue multiaxiale avec les critères de Dang Van ou de Zenner. Life assessment procedure under multiaxial constant amplitude fatigue by the use of Dang Van or Zenner criterion. |
| Dans le texte | |
 |
Fig. 13 Organigramme du calcul de durée de vie en fatigue multiaxiale avec le critère de Dang Van. Multiaxial fatigue life assessment according to Dang Van criterion. |
| Dans le texte | |
 |
Fig. 12 Concept mathématique de Simbüger pour examiner tous les plans matériels passant par un point matériel (ou nœud). Parametric definition of one material plane according to Simbürger denotations. |
| Dans le texte | |
 |
Fig. 14 Les zones critiques du rail en fatigue. Critical zones of the rail from the fatigue point of view. |
| Dans le texte | |
 |
Fig. 15 Cartographie de la durée de vie en fatigue (a) du rail, (b) de la vis. Fatigue life distribution (a) of the rail, (b) of the screw close to the assembly gap. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




