| Issue |
Matériaux & Techniques
Volume 105, Number 1, 2017
Indentation: fundamentals and developments
|
|
|---|---|---|
| Article Number | 103 | |
| Number of page(s) | 8 | |
| Section | Essais, mesure, contrôle non destructif / Testing, measurement and non destructive testing | |
| DOI | https://doi.org/10.1051/mattech/2017027 | |
| Published online | 23 June 2017 | |
Fluage et relaxation par indentation d’aciers au chrome
Creep and relaxation by indentation of chromium-based steels
1 Université de Lille, FRE 3723-LML-Laboratoire de Mécanique de Lille, Lille, France
2 Université de Lille, CNRS, INRA, ENSCL, UMR 8207 – UMET – Unité Matériaux et Transformations, 59000 Lille, France
3 Mines Douai, LGCgE, Douai, France
a Auteur de correspondance : nogningkamta@yahoo.fr
Reçu : 7 Décembre 2016
Accepté : 24 Mars 2017
L’étude du comportement en fluage et en relaxation de matériaux soumis à des conditions sévères en termes de température, de contrainte et de déformation est nécessaire mais parfois coûteuse avec les essais classiques. En effet, ces essais, particulièrement celui du fluage, sont très consommateurs de temps, ils peuvent durer plus d’une année. Pour ramener cette durée d’essais à quelques minutes, nous proposons d’utiliser l’indentation instrumentée qui, avec l’évolution des conditions d’application de la charge et du déplacement de l’indenteur, permet de solliciter le matériau dans des conditions de chargement proches de celles imposées dans les essais classiques. Dans cette étude, nous proposons d’étudier le comportement de deux aciers au chrome utilisés pour la fabrication d’appareils sous pression. Il s’agit des aciers à 9 % de chrome (T91) et à 2,5 % de chrome (T22), l’objectif étant de classer les matériaux selon leur sensibilité au fluage et à la relaxation. Dans ce travail, nous nous limitons à l’indentation à température ambiante pour étudier l’applicabilité de la technique d’indentation. En fluage, nous déterminons le coefficient de sensibilité à la contrainte et en relaxation le coefficient d’homothétie défini dans la théorie de Hart. L’intérêt de ces deux coefficients est qu’ils sont liés, l’un est l’inverse de l’autre, ce qui permet de comparer les deux modes de sollicitation.
Abstract
Study of creep and relaxation behaviours of materials submitted to severe conditions in terms of temperature, stress and strain is necessary but sometimes very expensive with classical tests. Indeed, these tests, mainly the creep one, are very time-consuming since it can last more than one year. In order to drastically reduce this duration, we suggest the use of the instrumented indentation test which allows testing the material with loading conditions comparable to that of the classical tests. This is now possible thanks to the development of the instrumented indentation. In this work, we propose to study the mechanical behaviour of two based chromium steels, 9 wt.% Cr (T91) and 2.5 wt.% Cr (T22), the objective being to classify the materials according to their creep and relaxation sensibilities. We limit our work to indentation experiments at room temperature in order to study the applicability of the indentation technique. With creep indentation, we determined the stress exponent and with relaxation by indentation the homothetic coefficient defined in the Hart’s theory. The main advantage to study these two coefficients is that there are linked by a simple relation, one being the reciprocal of the other, thus allowing to easily compare these two solicitation modes.
Mots clés : Fluage / relaxation / indentation / modélisation / aciers T91 et T22
Key words: Creep / relaxation / indentation / modeling / T22 and T91 steels
© EDP Sciences, 2017
1 Introduction
Le développement actuel des centrales thermiques passe par l’augmentation de la pression et de la température des gaz qui entrent dans les turbines. En effet, il a été montré qu’une légère augmentation de la température, de 580 à 600 °C seulement, conduit à une augmentation du rendement thermique de 38 à 42 % [1]. Une des conditions pour assurer cette augmentation passe par le choix du matériau le mieux adapté pour résister à ces conditions extrêmes de température et de pression, le matériau devant donc être très peu sensible au fluage à haute température. À cet effet, plusieurs nuances d’aciers au chrome ont été développées ces dernières décennies
pour répondre à ces exigences de tenue en service à la température de 600 °C[2, 3]. Pour étudier le comportement au fluage de ces aciers au chrome, plusieurs travaux s’appuient sur des essais classiques par traction uni-axiale [2, 3, 4]. Mais un des problèmes majeurs du point de vue de l’industrie est la durée des essais qui peut aller jusqu’à plus d’un an. L’essai classique est donc consommateur de temps et constitue de ce fait une perte d’argent.
Notre objectif n’est pas de déterminer des valeurs précises pour rendre compte du comportement en fluage mais il est de classer les matériaux selon leur sensibilité. Pour cela, nous proposons d’appliquer une méthodologie basée sur l’indentation instrumentée qui permet d’appliquer des conditions de chargement proches à l’essai classique. Notre étude est réalisée sur deux nuances d’aciers au chrome, à savoir l’acier 2,25Cr-1Mo (T22) et l’acier 9Cr-1Mo (T91) possédant des résistances au fluage différentes.
L’indentation instrumentée, principalement dével oppée pour la détermination de la dureté et du module d’élasticité [5, 6], est utilisée ici car elle permet de maintenir la charge appliquée pendant un temps donné durant lequel on constate dans la plupart des cas que l’indenteur continue à s’enfoncer. L’étude de la variation de la profondeur d’indentation en fonction du temps de maintien à chargement constant est typiquement représentatif d’un comportement au fluage [7, 8], que l’on prend bien soin ici d’appeler fluage par indentation puisqu’il ne peut en aucun cas se substituer à l’essai de fluage classique. Cette technique est particulièrement avantageuse dans la mesure où elle nécessite des échantillons de petites tailles, une préparation des échantillons moins contraignante, des durées d’essai plus courtes, une mise en œuvre plus simple et est non destructive. Plusieurs travaux proposent de représenter mathématiquement la relation profondeur-temps obtenue par indentation [9, 10, 11, 12, 13] qui peut ensuite être utilisée pour représenter la vitesse de déformation avec la contrainte appliquée. Il existe aussi d’autres techniques d’indentation [14, 15] permettant de remonter au coefficient de sensibilité à la contrainte en déterminant le coefficient de sensibilité à la vitesse de déformation : le jump test qui consiste à faire varier brusquement la vitesse de déformation pendant l’indentation et la technique consistant à indenter à différentes vitesses de déformation.
Dans une première partie, nous proposons donc de déterminer le coefficient de sensibilité à la contrainte en fluage à partir de la courbe vitesse de déformation – contrainte (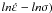 , après avoir défini les modalités d’application de la charge. Dans une seconde partie, nous proposons d’étudier le comportement en relaxation par indentation car il a été montré qu’il pouvait être utilisé pour classer les matériaux selon leur sensibilité au fluage [16, 17, 18]. À partir des travaux de Hart [19, 20], nous déterminons le coefficient d’homothétie déduit de la droite de translation permettant de construire une courbe maîtresse unique. L’intérêt de ce coefficient est qu’il est lié au coefficient de sensibilité à la contrainte obtenu par fluage, le premier étant l’inverse de l’autre. Cette comparaison doit nous amener à préciser lequel de ces deux modes de sollicitation est le plus fiable pour étudier la sensibilité au fluage et/ou en relaxation du matériau par indentation instrumentée.
, après avoir défini les modalités d’application de la charge. Dans une seconde partie, nous proposons d’étudier le comportement en relaxation par indentation car il a été montré qu’il pouvait être utilisé pour classer les matériaux selon leur sensibilité au fluage [16, 17, 18]. À partir des travaux de Hart [19, 20], nous déterminons le coefficient d’homothétie déduit de la droite de translation permettant de construire une courbe maîtresse unique. L’intérêt de ce coefficient est qu’il est lié au coefficient de sensibilité à la contrainte obtenu par fluage, le premier étant l’inverse de l’autre. Cette comparaison doit nous amener à préciser lequel de ces deux modes de sollicitation est le plus fiable pour étudier la sensibilité au fluage et/ou en relaxation du matériau par indentation instrumentée.
2 Matériaux et expérimentation
Les essais sont effectués sur deux nuances d’aciers au chrome, l’acier à 2,5 % de chrome (T22) et celui à 9 % (T91). Les compositions chimiques en pourcentage massique de ces deux matériaux sont données dans le Tableau 1 d’après [3, 21].
Composition chimique (%m) des aciers T22 et T91.
Chemical composition (wt.%) of T22 and T91 based chromium steels.
Les micrographies des microstructures [11] des deux matériaux révèlent une taille de grains d’environ 10μm pour le T91 et de 45μm pour le T22. Ces valeurs de grain sont largement inférieures à la diagonale moyenne de l’emprunt qui, dans le cadre de notre étude est située entre 48μ m et 175μm.
Les essais ont été réalisés à température ambiante, pour deux gammes de chargement, à l’aide d’une pointe Vickers en utilisant un microindenteur CSM2-107 de Anton Paar et un macroindenteur ZHU 2.5 de Zwick. La gamme de charge est de 0,1 à 25 N pour le microindenteur et de 5 à 2500 N pour le macroindenteur.
Pour le fluage par indentation, les essais en microindentation ont été effectués en tenant compte des conditions d’essais optimales que nous avons précédemment déterminées [11], à savoir une vitesse de chargement de 30 N/min, une charge de maintien supérieure à 3 N et un temps de maintien de 1000 s. Les conditions d’essais en relaxation réalisés en macroindentation ont été choisies en tenant compte de la vitesse d’approche de l’indenteur pour laquelle la vitesse de chargement doit être proche. La vitesse de chargement de 10 μm/min a été utilisée pour des profondeurs de maintien de 19, 20 et 25 μm. L’indenteur est maintenu à la profondeur maximale pendant 2000 s. La Figure 1 présente respectivement un exemple de courbes charge/déplacement relatives aux deux types d’essais.
 |
Fig. 1. Courbes typiques représentant la variation de la charge avec le déplacement de l’indenteur dans le cas (a) du fluage par microindentation et (b) de la relaxation par macroindentation. Typical load-displacement curves representative of (a) creep microindentation and (b) relaxation by macroindentation. |
Sur la Figure 1a, représentant l’essai de fluage par indentation, on observe un chargement suivi d’un maintien de 1000 s à la charge maximale puis d’une décharge. On constate que pendant le maintien, l’indenteur continue à s’enfoncer dans le matériau ce qui est caractéristique du fluage en indentation. Sur la Figure 1b, qui est représentative de la relaxation par indentation, on observe aussi un chargement suivi d’un maintien à une profondeur maximale pendant une durée de 2000 s avant le déchargement complet. Pendant le maintien à la profondeur maximale, la charge d’indentation diminue progressivement représentant la relaxation de la charge.
3 Étude du comportement au fluage par indentation
En indentation, deux approches mathématiques permettent de décrire le comportement au fluage des matériaux, l’une est basée sur la combinaison d’éléments rhéologiques et l’autre sur les lois phénoménologiques ou descriptives. Concernant les lois phénoménologiques, plusieurs modèles existent pour décrire la courbe de fluage par indentation, c’est-à-dire la variation de la profondeur avec le temps. On trouve par exemple les modèles proposés par Mahmundi et Rezaee-Bazzaz [10], Choi et al. [9] et Tabor [22]. De manière générale, le comportement mécanique des matériaux métalliques à une température donnée en fluage classique est décrit par une loi puissance entre la vitesse de déformation plastique et la contrainte appliquée. Dans ce cas, la vitesse de déformation, notée 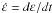 à l’état stationnaire, exprimée en fonction de la contrainte, σ, prend la forme générale suivante :
à l’état stationnaire, exprimée en fonction de la contrainte, σ, prend la forme générale suivante :  (1)Où A′ est un paramètre dépendant du matériau et n le coefficient de sensibilité à la contrainte.
(1)Où A′ est un paramètre dépendant du matériau et n le coefficient de sensibilité à la contrainte.
Le coefficient n est souvent utilisé comme indicateur du mécanisme de fluage prédominant pendant l’essai. Pour établir l’analogie entre le fluage classique et le fluage par indentation, il faut relier la contrainte de fluage à la dureté mesurée par indentation. Pour cela, Tabor [22] propose, pour un indenteur Vickers, l’expression de la contrainte caractéristique en fonction de la charge d’indentation et du déplacement de l’indenteur avec l’équation (2) :  (2)Où H est la dureté, P la charge d’indentation, Ac est l’aire de contact, qui est fonction de la profondeur de pénétration de l’indenteur et C la constante de Tabor.
(2)Où H est la dureté, P la charge d’indentation, Ac est l’aire de contact, qui est fonction de la profondeur de pénétration de l’indenteur et C la constante de Tabor.
De plus, Mayo et Nix [23] proposent de relier la vitesse de déformation caractéristique au déplacement de l’indenteur de la manière suivante : 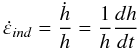 (3)Où ḣ est la vitesse de déplacement de l’indenteur et h le déplacement de l’indenteur.
(3)Où ḣ est la vitesse de déplacement de l’indenteur et h le déplacement de l’indenteur.
Pour calculer la vitesse de déplacement ḣ de l’indenteur, nous avons utilisé le modèle de Choi et al. [9] qui représente la variation de la profondeur d’empreinte en fonction du temps avec une loi additive de termes en puissance sous la forme : 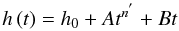 (4)Où A, B et n sont les paramètres de lissage des courbes expérimentales.
(4)Où A, B et n sont les paramètres de lissage des courbes expérimentales.
Cette relation permet de calculer en tout point la dérivée de la fonction h(t) et ainsi d’exprimer la vitesse de déformation par indentation à partir de la relation (3), soit : ![\begin{equation} \label{eq5} \Dot{\varepsilon }_{ind}=\frac{1}{h} \, [An'\, t^{n'-1}+B] \end{equation}](/articles/mattech/full_html/2017/01/mt160103/mt160103-eq26.png) (5)Ainsi, l’équation (1) adaptée au cas du fluage par indentation permet de relier directement la vitesse de déformation par indentation de l’équation (3) à la dureté de l’équation (2) par un coefficient de proportionnalité Γ:
(5)Ainsi, l’équation (1) adaptée au cas du fluage par indentation permet de relier directement la vitesse de déformation par indentation de l’équation (3) à la dureté de l’équation (2) par un coefficient de proportionnalité Γ: 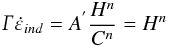 (6)Le calcul du coefficient de sensibilité à la contrainte, n, se détermine directement de l’équation (6) par la relation :
(6)Le calcul du coefficient de sensibilité à la contrainte, n, se détermine directement de l’équation (6) par la relation : 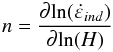 (7)En pratique, on peut tracer l’évolution de la profondeur de pénétration de l’indenteur en fonction du temps de maintien à partir des données obtenues pendant le maintien à la charge maximale. Pour étudier la reproductibilité des essais de fluage par indentation, nous avons réalisé 10 essais par condition. La Figure 2 représente l’ensemble des courbes de fluage obtenues avec une charge maximale de maintien de 10 N et un temps de maintien de 1000 s. Nous remarquons que les courbes sont très sensibles à la localisation de l’essai. Pour obtenir une valeur moyenne représentative de l’essai, nous travaillons sur la courbe moyenne.
(7)En pratique, on peut tracer l’évolution de la profondeur de pénétration de l’indenteur en fonction du temps de maintien à partir des données obtenues pendant le maintien à la charge maximale. Pour étudier la reproductibilité des essais de fluage par indentation, nous avons réalisé 10 essais par condition. La Figure 2 représente l’ensemble des courbes de fluage obtenues avec une charge maximale de maintien de 10 N et un temps de maintien de 1000 s. Nous remarquons que les courbes sont très sensibles à la localisation de l’essai. Pour obtenir une valeur moyenne représentative de l’essai, nous travaillons sur la courbe moyenne.
 |
Fig. 2. Exemples de courbes de fluage, déplacement-temps, obtenues par indentation de l’acier T91 à la charge maximale de 10 N. Examples of creep curves, displacement-time, obtained by indentation of the based chromium steel T91 steel under the maximum load of 10 N. |
La Figure 3 représente les courbes moyennes de fluage obtenues par indentation des aciers T22 (Fig. 3a) et T91 (Fig. 3b) aux charges de maintien de 3, 5, 10 et 15 N.
 |
Fig. 3. Variation de la profondeur d’indentation en fonction du temps de maintien à la charge maximale pour les aciers a) T22 et b) T91. Indenter displacement versus the time duration at the maximum load for the based chromium steels a) T22 and b) T91. |
Contrairement aux courbes de fluage obtenues par des essais classiques qui présentent généralement trois stades de fluage (primaire ou instantané, secondaire ou stationnaire et tertiaire ou de rupture), les courbes de fluage obtenues par indentation ne présentent évidemment que les deux premiers stades de fluage. La première partie de la courbe dite de fluage primaire correspond à une augmentation rapide du déplacement de l’indenteur qui s’accompagne de la diminution de la vitesse d’indentation jusqu’à atteindre une valeur constante. À partir de cette valeur constante, nous entrons dans le stade de fluage stationnaire qui correspond à la variation linéaire de la profondeur de pénétration en fonction du temps. L’absence du troisième stade ici est due au fait qu’en indentation, on ne peut observer de rupture du matériau. On note aussi sur la Figure 3 que la profondeur augmente logiquement avec la charge de maintien. En comparant les comportements des deux matériaux (Figs. 3a et 3b), on constate que pour une même charge de maintien, la profondeur de pénétration est plus élevée pour l’acier T22 que pour l’acier T91. Ceci montre à l’évidence que l’acier T91 est plus résistant au fluage primaire que l’acier T22, au moins à cette température.
Le coefficient de sensibilité à la contrainte, que nous cherchons à obtenir, est déterminé en traçant la variation de la vitesse de déformation en fonction de la dureté dans un graphe bi-logarithmique, la pente de cette courbe étant le coefficient de sensibilité comme le montre la Figure 4. Le calcul de la pente est réalisé au début de la courbe correspondant au régime stationnaire du fluage de la courbe charge-décharge.
Le Tableau 2 rassemble les valeurs du coefficient de sensibilité à la contrainte obtenues pour les aciers T22 et T91 à température ambiante pour différentes charges de maintien. Les variations que nous constatons sur les coefficients de sensibilité viennent en partie des variations observées sur les courbes de fluage comme le montre la Figure 2.
 |
Fig. 4. Vitesse de déformation caractéristique en fonction de la dureté dans un graphe bi-logarithmique pour plusieurs charges de maintien, pour l’acier T91. Strain rate versus hardness in bi-logarithmic coordinates for several maximum creep loads, for T91 steel. |
Coefficients de sensibilité à la contrainte des aciers T22 et T91 obtenus pour différentes charges de maintien.
Stress exponent for the based chromium steels T22 and T91 obtained for different maximum loads.
4 Étude du comportement en relaxation par indentation
Pendant un essai de relaxation, la déformation est imposée et maintenue constante. La contrainte générée au début de l’essai par l’application de la déformation tend ensuite à décroitre au cours du temps, c’est la relaxation de la contrainte. La déformation totale constante se décompose en un terme plastique εp et un terme élastique εe dont la somme reste constante au cours du temps, soit : 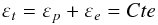 (8)En dérivant l’équation (8) par rapport au temps, on peut exprimer la vitesse de déformation plastique comme étant l’opposée de la vitesse de déformation élastique.
(8)En dérivant l’équation (8) par rapport au temps, on peut exprimer la vitesse de déformation plastique comme étant l’opposée de la vitesse de déformation élastique.
Du point de vue de la relaxation de la contrainte, l’étude par indentation peut se faire à partir de la charge ou de la contrainte d’indentation étant donné que la charge est reliée à la dureté (contrainte) par la relation H = P/Ac. En utilisant la relation de Tabor, équation (2), exprimant la contrainte en fonction de la dureté et en considérant la loi de Hooke reliant la contrainte à la déformation élastique (σ = Eε), on peut relier la vitesse de déformation plastique à la contrainte de relaxation σ et au module d’élasticité E par la relation : 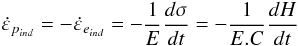 (9)Pour connaître la variation de la dureté en fonction du temps, on peut utiliser deux approches mathématiques initialement développées pour représenter la contrainte de relaxation en essai classique, soit la relation logarithmique proposée par Trouton et Rankine [24] (Eq. (10)), soit la loi puissance proposée par Li [25] (Eq. (11)). Ces lois ont été adaptées au cas de la relaxation par indentation en remplaçant simplement la contrainte par la dureté :
(9)Pour connaître la variation de la dureté en fonction du temps, on peut utiliser deux approches mathématiques initialement développées pour représenter la contrainte de relaxation en essai classique, soit la relation logarithmique proposée par Trouton et Rankine [24] (Eq. (10)), soit la loi puissance proposée par Li [25] (Eq. (11)). Ces lois ont été adaptées au cas de la relaxation par indentation en remplaçant simplement la contrainte par la dureté :  (10)Où H0 serait la dureté au début de la relaxation, α et β sont des constantes
(10)Où H0 serait la dureté au début de la relaxation, α et β sont des constantes  (11)Où C,D et m sont des paramètres ajustables et Hi la dureté interne définie par Li [23].
(11)Où C,D et m sont des paramètres ajustables et Hi la dureté interne définie par Li [23].
La loi logarithmique est la plus utilisée des deux pour représenter les courbes de relaxation de la contrainte, mais elle présente des limites car elle ne donne pas une bonne représentation des données expérimentales pour des essais de très longue durée. Pour la loi en puissance, elle représente mieux les courbes obtenues pour des essais de longue durée car elle possède trois coefficients de lissage au lieu de deux. Dans notre étude, nous n’avons pas réussi à lisser correctement les points expérimentaux avec l’une ou l’autre de ces relations. C’est pourquoi nous proposons d’utiliser une relation similaire à celle proposée par Choi et al. [9] en fluage sous la forme :  (12)Où A2,n2 et B2 sont des paramètres ajustables.
(12)Où A2,n2 et B2 sont des paramètres ajustables.
Pour étudier le comportement en relaxation, Hart [19, 20] a développé une théorie pour initialement décrire la déformation plastique intragranulaire d’un solide polycristallin soumis à une traction monotone. Ce modèle est fondé sur l’existence d’une relation constitutive reliant la contrainte, la vitesse de déformation non élastique avec le paramètre de dureté qui gouverne le comportement inélastique du matériau. Cette relation est applicable aux essais réalisés par indentation car la contrainte et la vitesse de déformation plastique sont accessibles par cet essai. Dans son énoncé, Hart constate que les courbes contrainte/déformation réalisées pour différents taux de déformation présentent une relation d’échelle et propose une méthodologie permettant de tracer une courbe maîtresse représentative du comportement global du matériau obtenue en translatant les courbes selon une droite dont la pente s’exprime par la relation :  (13)Où
(13)Où 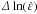 et
et  sont respectivement l’abscisse et l’ordonné du vecteur de translation dans le plan (O,
sont respectivement l’abscisse et l’ordonné du vecteur de translation dans le plan (O, 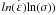 .
.
Il est intéressant de noter que dans plusieurs travaux, et en particulier ceux de Hart et Harvey [17] sur l’aluminium polycristallin la valeur de la pente de translation μ est équivalente à l’inverse du coefficient de sensibilité à la contrainte obtenu par fluage classique. Ce coefficient peut alors être utilisé pour établir un lien entre fluage et relaxation. Nous allons voir dans cette étude, si ce passage est vérifié.
À partir de la période de relaxation des courbes d’indentation (Partie verticale de la Fig. 1b), nous pouvons tracer l’évolution de la charge d’indentation ou de la dureté en fonction du temps. Comme dans le cas des essais de fluage, nous avons réalisé 10 essais par condition d’indentation de manière à obtenir une courbe moyenne représentative du comportement en relaxation. La Figure 5 montre les courbes de relaxation de la contrainte caractéristique de l’acier T91 obtenues à une profondeur maximale maintenue à 20 μm pendant 2000 s. Dans ce cas, nous constatons aussi une sensibilité des essais de relaxation par rapport à leur localisation à la surface du matériau.
 |
Fig. 5. Variation de la dureté en fonction du temps dans le cas de la relaxation de l’acier T91 pour une profondeur d’indentation maintenue à 20 μm. Hardness variation as a function of time for the relaxation of the T91 chromium based steel at the indenter depth of 20 μm. |
La Figure 6 représente une courbe moyenne de relaxation de la dureté obtenue pour l’acier T91 à la profondeur de maintien de 20 μm.
 |
Fig. 6. Variation de la dureté en fonction du temps dans le cas de la relaxation de l’acier T91 pour une profondeur d’indentation maintenue à 20 μm. Hardness variation as a function of time for the relaxation of the T91 chromium based steel at the indenter depth of 20 μm. |
Il est intéressant de noter que l’allure générale d’une courbe de relaxation obtenue par indentation suit une forme similaire à celle qui serait obtenue en traction uni-axiale. Il est également à noter que l’équation (12) que nous proposons pour représenter la variation de la contrainte en fonction du temps ajuste très bien la courbe de relaxation avec un coefficient de corrélation proche de 1. La Figure 6 représente les courbes de relaxation de la charge d’indentation de l’acier T91 obtenues à trois profondeurs de maintien. Comme il est attendu, le niveau de chargement est plus élevé lorsqu’on impose une profondeur de maintien plus grande. On observe aussi une forte décroissance de la charge dès le début de la relaxation.
 |
Fig. 7. Courbes de relaxation de la charge d’indentation pour plusieurs profondeurs de maintien pour l’acier T91. Relaxation curves representing the indentation load versus time for several indenter displacements for the based chromium steel T91. |
Nous appliquons maintenant le modèle de Hart à ces résultats de manière à remonter à la pente de la droite de translation utilisée pour construire la courbe maîtresse selon Hart. La Figure 8a représente dans une échelle bi-logarithmique l’évolution de la dureté en fonction de la vitesse de déformation plastique pour trois profondeurs de maintien.
 |
Fig. 8. (a) Variation de la dureté en fonction de la vitesse de déformation plastique à trois profondeurs de maintien et (b) Courbe maîtresse selon la méthode de Hart pour l’acier T91. (a) Hardness variation as a function of the plastic deformation rate for three indenter displacements and (b) Unique curve according to the methodology of Hart for the based chromium steel T91. |
La Figure 8a montre très clairement une relation d’échelle entre ces différentes courbes. A partir de la méthodologie développée par Hart, nous construisons la courbe maîtresse par translation comme le montre la Figure 8a. La droite de translation relie les points de chaque courbe ayant la même pente. La courbe maitresse ainsi construite est constituée d’un segment de chaque courbe translatée. La pente de la droite de translation μ vaut 0,0327. La Figure 8b représente la courbe maîtresse obtenue en translatant les deux premières courbes (relatives aux profondeurs les plus faibles) sur la troisième (relative à la profondeur la plus élevée). L’intérêt de la courbe maîtresse est de pouvoir étudier le comportement du matériau sur un plus large domaine de déformation. L’autre avantage est d’utiliser la pente de la droite de translation pour comparer avec l’étude du fluage. Ici, pour l’acier T91, la valeur du coefficient de sensibilité au fluage déduit de la pente de translation nous donne n = 1 /μ = 31 qui doit être comparée à la valeur de 48 que nous avons trouvés en fluage par indentation (Tab. 2). Pour l’acier T22, le coefficient n par fluage est de 75 et par relaxation à partir du coefficientμ, il n’est que de 15. Bien que les valeurs obtenues par les deux modes de sollicitation en indentation soient à l’évidence très différentes, nous pensons que cette approche reste intéressante mais que toutefois des études complémentaires doivent être menées autant sur la répétabilité des essais, que sur l’effet de la température et la méthode de translation des courbes en relaxation amenant à la détermination du coefficient μ.
5 Conclusions
Nous avons défini ici les conditions d’application de la charge et du déplacement de l’indenteur dans les essais de fluage et de relaxation par indentation. Les courbes charge-décharge semblent très sensibles à la localisation de l’essai, c’est pourquoi nous préconisons de répéter les essais au moins 10 fois par condition. À partir des courbes moyennes obtenues, nous proposons d’appliquer le modèle de Choi pour décrire la variation de la profondeur en fonction du temps dans le cas du fluage et de la dureté en fonction du temps dans le cas de la relaxation. Ce modèle permet de bien représenter les points expérimentaux avec une très grande précision puisque le coefficient de corrélation est pratiquement égal à 1. Notons que les autres modèles disponibles dans la littérature, même si apparemment ils représenteraient correctement l’évolution des points expérimentaux, ne permettent pas d’appliquer valablement la théorie de Hart suite aux incertitudes dans le calcul de la vitesse de déformation plastique. Les courbes contrainte - vitesse de déformation plastique obtenues à partir de ces modèles ne sont plus homothétiques et, par conséquent, il n’est pas possible d’obtenir une courbe maîtresse.
Nous avons déterminé à température ambiante le coefficient de sensibilité à la contrainte par fluage et par relaxation à partir d’essais d’indentation en nous appuyant sur la théorie de Hart pour les essais de relaxation. Bien que les valeurs des coefficients trouvées par les deux modes de sollicitation par indentation soient différentes, cette approche nous apparait très encourageante. Toutefois, des études complémentaires autant sur le fluage que sur la relaxation par indentation sont nécessaires. Les points à aborder sont relatifs à la reproductibilité des essais et à la description mathématique des phénomènes mis en jeu. Les essais doivent aussi être validés à haute température pour s’approcher des conditions d’utilisation des aciers au chrome. Notons également que le classement des matériaux selon leur sensibilité à ce mode de sollicitation peut changer en fonction de la température de l’étude.
References
- D.H. Allen, J.E. Oakey, and B. Scarlin, The new COST action 522-power generation in the 21st century: ultra-efficient, low-emission plant, ibid, pp. 1825-1839 [Google Scholar]
- F. Abe, Curr. Opin. Solid State Mater. Sci. 8 (2004) 305-311 [CrossRef] [Google Scholar]
- D. Dugre, J.C. Vaillant, F. Pellicani, M. Julien, The P91 Book - Ferritic Pipe for High Temperature use in Boilers and petrochemical applications. (Publ. Vallourec Industries, 1992) [Google Scholar]
- K. Kimura, H. Kushima, K. Sawada, Mater. Sci. Eng. A 510-511 (2009) 58-63 [CrossRef] [Google Scholar]
- A. Tricoteaux, G. Duarte, D. Chicot, E. Le Bourhis, E. Bemporad, J. Lesage, Mech. Mater. 42 (2010) 166-174 [CrossRef] [Google Scholar]
- W.C. Oliver, G.M. Pharr, J. Mater. Res. 19 (2004) 3-20 [Google Scholar]
- Y. Hu, J.-O. You, D. T. Auguste, Z. Suo, J. J. Vlassak, J. Mater. Res. 27 (2012) 152-160 [CrossRef] [Google Scholar]
- W. R. LaFontaine, B. Yost, R. D. Black, C.-Y. Li, J. Mater. Res. 5 (1990) 2100-2106 [CrossRef] [Google Scholar]
- I.C. Choi, B.G. Yoo, Y.J. Kim, M.Y. Seok, Y. Wang, J.I. Jang, Scr. Mater. 65 (2011) 300-303 [CrossRef] [Google Scholar]
- R. Mahmudi, A. Rezaee-Bazzaz, Mater. Lett. 59 (2005) 1705-1708 [CrossRef] [Google Scholar]
- P. Nogning Kamta, A. Mejias, F. Roudet, G. Louis, M. Touzin, D. Chicot, Mater. Sci. Eng. A 652 (2016) 315-324 [CrossRef] [Google Scholar]
- A.C. Fischer-Cripps, Mater. Sci. Eng. A 385 (2004) 74-82 [CrossRef] [Google Scholar]
- D. Chicot, D. Mercier, Mech. Mater. 40 (2008) 171-182 [CrossRef] [Google Scholar]
- R. Kasada, S. Konishi, D. Hamaguchi, M. Ando, H. Tanigawa, Fusion Eng. Des. 109-111 (2016) 1507-1510 [CrossRef] [Google Scholar]
- R. Schwaiger, B. Moser, M. Dao, N. Chollacoop, S. Suresh, Acta Mater. 51 (2003) 5159-5172 [CrossRef] [Google Scholar]
- M. F. Felsen, J. Tortel, Creep under variable stress-creep under increasing stress-creep during relaxation. Annales de chimie-science des matériaux 6 (2), 120 Bd Saint-Germain, 75280 Paris 06, France: Masson Editeur, (1981) 140-149 [Google Scholar]
- D. Stone, H. Wilson, R.C. Kuo, C.Y. Li, Scripta Metall. 21 (1987) 1559-1563 [CrossRef] [Google Scholar]
- J. Lemaître, J.L. Chaboche, Mécanique des matériaux solides. Edition Dunod, 2004 [Google Scholar]
- E.W. Hart, H.D. Solomon, Acta Metall. 21 (1973) 295-307 [CrossRef] [Google Scholar]
- H. Garmestani, M.R. Vaghar, E.W. Hart, Int. J. Plast. 17 (2001) 1367-1391 [CrossRef] [Google Scholar]
- J. Arndt, F. Deshayes, W. Bendick, J.C. Vaillant, G. Kottmann, K. Haarmann, The T23/T24 Book (Vallourec & Mannesmann Tubes, 1998) [Google Scholar]
- D. Tabor, J. Inst. Met. 79 (1951) 1-18 [Google Scholar]
- M.J. Mayo, W.D. Nix, Acta Metall. 36 (1988) 2183-2192 [CrossRef] [Google Scholar]
- F.R.S. Trouton, A.O. Rankine LII Philos. Mag. Series 6 (1904) 538-556 [CrossRef] [Google Scholar]
- J.C.M Li, Can. J. Phys. 45 (1967) 493-509 [CrossRef] [Google Scholar]
Liste des tableaux
Composition chimique (%m) des aciers T22 et T91.
Chemical composition (wt.%) of T22 and T91 based chromium steels.
Coefficients de sensibilité à la contrainte des aciers T22 et T91 obtenus pour différentes charges de maintien.
Stress exponent for the based chromium steels T22 and T91 obtained for different maximum loads.
Liste des figures
 |
Fig. 1. Courbes typiques représentant la variation de la charge avec le déplacement de l’indenteur dans le cas (a) du fluage par microindentation et (b) de la relaxation par macroindentation. Typical load-displacement curves representative of (a) creep microindentation and (b) relaxation by macroindentation. |
| Dans le texte | |
 |
Fig. 2. Exemples de courbes de fluage, déplacement-temps, obtenues par indentation de l’acier T91 à la charge maximale de 10 N. Examples of creep curves, displacement-time, obtained by indentation of the based chromium steel T91 steel under the maximum load of 10 N. |
| Dans le texte | |
 |
Fig. 3. Variation de la profondeur d’indentation en fonction du temps de maintien à la charge maximale pour les aciers a) T22 et b) T91. Indenter displacement versus the time duration at the maximum load for the based chromium steels a) T22 and b) T91. |
| Dans le texte | |
 |
Fig. 4. Vitesse de déformation caractéristique en fonction de la dureté dans un graphe bi-logarithmique pour plusieurs charges de maintien, pour l’acier T91. Strain rate versus hardness in bi-logarithmic coordinates for several maximum creep loads, for T91 steel. |
| Dans le texte | |
 |
Fig. 5. Variation de la dureté en fonction du temps dans le cas de la relaxation de l’acier T91 pour une profondeur d’indentation maintenue à 20 μm. Hardness variation as a function of time for the relaxation of the T91 chromium based steel at the indenter depth of 20 μm. |
| Dans le texte | |
 |
Fig. 6. Variation de la dureté en fonction du temps dans le cas de la relaxation de l’acier T91 pour une profondeur d’indentation maintenue à 20 μm. Hardness variation as a function of time for the relaxation of the T91 chromium based steel at the indenter depth of 20 μm. |
| Dans le texte | |
 |
Fig. 7. Courbes de relaxation de la charge d’indentation pour plusieurs profondeurs de maintien pour l’acier T91. Relaxation curves representing the indentation load versus time for several indenter displacements for the based chromium steel T91. |
| Dans le texte | |
 |
Fig. 8. (a) Variation de la dureté en fonction de la vitesse de déformation plastique à trois profondeurs de maintien et (b) Courbe maîtresse selon la méthode de Hart pour l’acier T91. (a) Hardness variation as a function of the plastic deformation rate for three indenter displacements and (b) Unique curve according to the methodology of Hart for the based chromium steel T91. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




